题目内容
已知e为自然对数的底数，设函数f(x)＝(ex－1)(x－1)k(k＝1,2)，则( )
A．当k＝1时，f(x)在x＝1处取到极小值
B．当k＝1时，f(x)在x＝1处取到极大值
C．当k＝2时，f(x)在x＝1处取到极小值
D．当k＝2时，f(x)在x＝1处取到极大值
C
[解析] 本题考查函数零点的判断及函数的极值．
①当k＝1时，f(x)＝(ex－1)(x－1)，此时f ′(x)＝ex(x－1)＋(ex－1)＝ex·x－1，∴A、B项均错．
②当k＝2时，f(x)＝(ex－1)(x－1)2
此时f ′(x)＝ex(x－1)2＋(2x－2)(ex－1)
＝ex·x2－2x－ex＋2＝ex(x＋1)(x－1)－2(x－1)
＝(x－1)[ex(x＋1)－2]，
易知g(x)＝ex(x＋1)－2的零点介于0,1之间，不妨设为x0，则有
| x | (－∞，x0) | x0 | (x0,1) | 1 | (1，＋∞) |
| f ′(x) | ＋ | 0 | － | 0 | ＋ |
| f(x) | | 极大值 | ↘ | 极小值 | |
练习册系列答案
名校课堂系列答案
相关题目
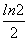D．ln2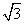
)，那么曲线y＝f(x)上任一点的切线的倾斜角α的取值范围是( )
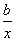，曲线y＝f(x)在点(2，f(2))处的切线方程为7x－4y－12＝0.
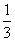x3＋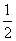
x2＋2ax.
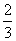，＋∞)上存在单调递增区间，求a的取值范围．
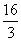，求f(x)在该区间上的最大值．
，α∈(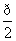
，π)，则cosα＝________.