题目内容
已知f(x)＝xlnx，若f ′(x0)＝2，则x0＝( )
A．e2 B．e
C.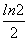
D．ln2
B
[解析] f(x)的定义域为(0，＋∞)，f ′(x)＝lnx＋1，
由f ′(x0)＝2，即lnx0＋1＝2，解得x0＝e.
练习册系列答案
步步高达标卷系列答案
相关题目
步步高达标卷系列答案题目内容
已知f(x)＝xlnx，若f ′(x0)＝2，则x0＝( )
A．e2 B．e
C.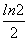 D．ln2
B
[解析] f(x)的定义域为(0，＋∞)，f ′(x)＝lnx＋1，
由f ′(x0)＝2，即lnx0＋1＝2，解得x0＝e.
步步高达标卷系列答案
，且过点(4，－
)．
·
＝0；