题目内容
设f(x)=-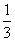 x3+
x3+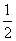 x2+2ax.
x2+2ax.
(1)若f(x)在(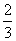 ,+∞)上存在单调递增区间,求a的取值范围.
,+∞)上存在单调递增区间,求a的取值范围.
(2)当0<a<2时,f(x)在[1,4]上的最小值为-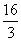 ,求f(x)在该区间上的最大值.
,求f(x)在该区间上的最大值.
(1)由f ′(x)=-x2+x+2a
=-(x-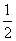 )2+
)2+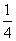 +2a
+2a
当x∈[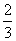 ,+∞)时,f ′(x)的最大值为f ′(
,+∞)时,f ′(x)的最大值为f ′(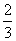 )=
)=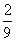 +2a;令
+2a;令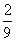 +2a>0,得a>-
+2a>0,得a>-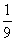
所以,当a>-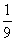 时,f(x)在(
时,f(x)在(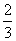 ,+∞)上存在单调递增区间.即f(x)在(
,+∞)上存在单调递增区间.即f(x)在(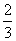 ,+∞)上存在单调递增区间时,a的取值范围是(-
,+∞)上存在单调递增区间时,a的取值范围是(-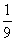 ,+∞).
,+∞).
(2)令f ′(x)=0,得两根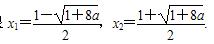
所以f(x)在(-∞,x1),(x2,+∞)上单调递减,
在(x1,x2)上单调递增.
当0<a<2时,有x1<1<x2<4,
所以f(x)在[1,4]上的最大值为f(x2),
又f(4)-f(1)=-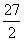 +6a<0,即f(4)<f(1)
+6a<0,即f(4)<f(1)
所以f(x)在[1,4]上的最小值为f(4)=8a-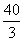 =-
=-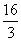 ,得a=1,x2=2,
,得a=1,x2=2,
从而f(x)在[1,4]上的最大值为f(2)=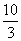 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
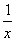 )的大小关系;
)的大小关系;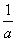 对任意x>0成立.
对任意x>0成立.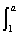 (2x+
(2x+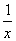 )dx=3+ln2,且a>1,则a的值为( )
)dx=3+ln2,且a>1,则a的值为( )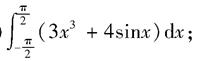
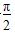 D
D