题目内容
已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.
(1)求a,b的值;
(2)讨论f(x)的单调性,并求f(x)的极大值.
[解析] (1)f ′(x)=ex(ax+a+b)-2x-4.
由已知得f(0)=4,f ′(0)=4,故b=4,a+b=8.
从而a=4,b=4.
(2)由(1)知,f(x)=4ex(x+1)-x2-4x,
f ′(x)=4ex(x+2)-2x-4=4(x+2)(ex-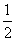 ).
).
令f ′(x)=0得,x=-ln2或x=-2.
从而当x∈(-∞,-2)∪(-ln2,+∞)时,f ′(x)>0;
当x∈(-2,-ln2)时,f ′(x)<0.
故f(x)在(-∞,-2),(-ln2,+∞)上单调递增,
在(-2,-ln2)上单调递减.
当x=-2时,函数f(x)取得极大值,
极大值为f(-2)=4(1-e-2).

练习册系列答案
相关题目
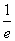 D.a<-
D.a<-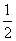 sin2x+sinx,则f ′(x)是( )
sin2x+sinx,则f ′(x)是( )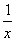 )的大小关系;
)的大小关系;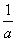 对任意x>0成立.
对任意x>0成立.