题目内容
已知函数f(x)=ax-lnx,若f(x)>1在区间(1,+∞)内恒成立,则实数a的取值范围为________.
a≥1
[解析] 由已知得a>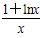 在区间(1,+∞)内恒成立.
在区间(1,+∞)内恒成立.
设g(x)=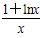 ,则g′(x)=-
,则g′(x)=-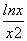 <0 (x>1),
<0 (x>1),
∴g(x)=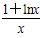 在区间(1,+∞)内单调递减,
在区间(1,+∞)内单调递减,
∴g(x)<g(1),∵g(1)=1,
∴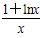 <1在区间(1,+∞)内恒成立,∴a≥1.
<1在区间(1,+∞)内恒成立,∴a≥1.

练习册系列答案
相关题目
题目内容
已知函数f(x)=ax-lnx,若f(x)>1在区间(1,+∞)内恒成立,则实数a的取值范围为________.
a≥1
[解析] 由已知得a>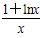 在区间(1,+∞)内恒成立.
在区间(1,+∞)内恒成立.
设g(x)=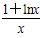 ,则g′(x)=-
,则g′(x)=-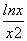 <0 (x>1),
<0 (x>1),
∴g(x)=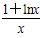 在区间(1,+∞)内单调递减,
在区间(1,+∞)内单调递减,
∴g(x)<g(1),∵g(1)=1,
∴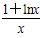 <1在区间(1,+∞)内恒成立,∴a≥1.
<1在区间(1,+∞)内恒成立,∴a≥1.
