题目内容
17.已知直三棱柱ABC-A1B1C1的所有棱长都为2,点P,Q分别为棱CC1,BC的中点,则四面体A1-B1PQ的体积为$\frac{\sqrt{3}}{2}$.分析 以A为原点,在平面ABC中过A作AC的垂线为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出四面体A1-B1PQ的体积.
解答  解:以A为原点,在平面ABC中过A作AC的垂线为x轴,AC为y轴,AA1为z轴,
解:以A为原点,在平面ABC中过A作AC的垂线为x轴,AC为y轴,AA1为z轴,
建立空间直角坐标系,
A1(0,0,2),B1($\sqrt{3}$,1,2),
Q($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$,0),P(0,2,1),
$\overrightarrow{P{B}_{1}}$=($\sqrt{3}$,-1,1),
$\overrightarrow{PQ}$=($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,-1),$\overrightarrow{P{A}_{1}}$=(0,-2,1),
设平面PQB1的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PQ}=\frac{\sqrt{3}}{2}x-\frac{1}{2}y-z=0}\\{\overrightarrow{n}•\overrightarrow{P{B}_{1}}=\sqrt{3}x-y+z=0}\end{array}\right.$,
取x=1,得$\overrightarrow{n}$=(1,$\sqrt{3}$,0),
∴A1平面PQB1的距离d=$\frac{|\overrightarrow{P{A}_{1}}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
|$\overrightarrow{PQ}$|=$\sqrt{\frac{3}{4}+\frac{1}{4}+1}$=$\sqrt{2}$,|$\overrightarrow{P{B}_{1}}$|=$\sqrt{3+1+1}$=$\sqrt{5}$,
cos<$\overrightarrow{PQ},\overrightarrow{P{B}_{1}}$>=$\frac{\overrightarrow{PQ}•\overrightarrow{P{B}_{1}}}{|\overrightarrow{PQ}|•|\overrightarrow{P{B}_{1}}|}$=$\frac{\frac{3}{2}+\frac{1}{2}-1}{\sqrt{2}•\sqrt{5}}$=$\frac{1}{\sqrt{10}}$,
sin<$\overrightarrow{PQ},\overrightarrow{P{B}_{1}}$>=$\sqrt{1-\frac{1}{10}}$=$\frac{3}{\sqrt{10}}$,
∴${S}_{△PQ{B}_{1}}$=$\frac{1}{2}×|\overrightarrow{PQ}|×|\overrightarrow{P{B}_{1}}|×sin<\overrightarrow{PQ},\overrightarrow{P{B}_{1}}>$=$\frac{1}{2}×\sqrt{2}×\sqrt{5}×\frac{3}{\sqrt{10}}$=$\frac{3}{2}$,
∴四面体A1-B1PQ的体积为:
V=$\frac{1}{3}×d×{S}_{△PQ{B}_{1}}$=$\frac{1}{3}×\sqrt{3}×\frac{3}{2}$=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查几何体的体积、空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、空间想象能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案| A. | AB边中线所在的直线上 | B. | ∠C平分线所在的直线上 | ||
| C. | 与AB垂直的直线上 | D. | 三角形ABC的外心 |
| A. | 若l⊥m,m⊆α则l⊥α | B. | 若l∥α,m⊆α则l∥m | C. | 若l⊥α,l∥m则m⊥α | D. | 若l∥α,m∥α则l∥m |
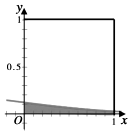 在如图所示的正方形中随机选择10000个点,则选点落入阴影部分(边界曲线C为正态分布N(-1,1)的密度曲线的一部分)的点的个数的估计值为( )
在如图所示的正方形中随机选择10000个点,则选点落入阴影部分(边界曲线C为正态分布N(-1,1)的密度曲线的一部分)的点的个数的估计值为( )附:若X:N(μ,δ2),则P(μ-δ<X≤μ+δ)=0.6826.P(μ-δ<X≤μ+2δ)=0.9544.
| A. | 906 | B. | 1359 | C. | 2718 | D. | 3413 |
| A. | [-2,1] | B. | [-2,2] | C. | [-2,3] | D. | [-2,4] |
| A. | $\frac{1}{3}$ | B. | $\frac{3}{π}$ | C. | 3 | D. | 6 |
| A. | 1-2i | B. | -5 | C. | 5 | D. | 5i |