题目内容
3.求函数f(x)=2x2-lnx的单调区间.分析 先求函数的定义域,再求导数,令导数大于0,解得x的范围即为函数的单调增区间.然后求解单调减区间.
解答 解:函数f(x)=2x2-lnx的定义域为(0,+∞)
对函数f(x)=2x2-lnx求导,得f′(x)=4x-$\frac{1}{x}$,
令f′(x)>0,∵x>0,∴得4x-$\frac{1}{x}$>0,解得,x>$\frac{1}{2}$,
∴函数的单调增区间为($\frac{1}{2}$,+∞).
单调减区间为:(0,$\frac{1}{2}$).
点评 本题主要考查利用导数求函数的单调区间,易错点是忘记求函数的定义域.

练习册系列答案
相关题目
15.执行右面的程序框图,如果输出的a值大于2017,那么判断框内的条件为( )

| A. | k<9? | B. | k≥9? | C. | k<10? | D. | k≥11? |
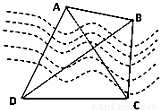
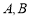 两点都在河的对岸(不可到达),为了测量
两点都在河的对岸(不可到达),为了测量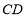 ,测得:
,测得: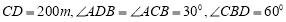 ,则
,则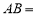 ()
()
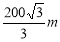 B.
B.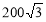
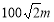 D.数据不够,无法计算
D.数据不够,无法计算 ,那么下面不等式一定成立的是( )
,那么下面不等式一定成立的是( ) B.
B. C.
C. D.
D.