题目内容
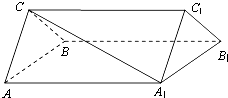如图，三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°，E为BC中点（Ⅰ）证明：A1C∥平面AB1E
（Ⅱ）证明：AB⊥A1C．
考点：直线与平面平行的判定,空间中直线与直线之间的位置关系
专题：证明题,空间位置关系与距离
分析：（Ⅰ）连结A1B，使A1B∩AB1=O，连结EO，由已知可证明EO∥A1C，又因为EO?平面AB1E，A1C?平面AB1E，即可判定A1C∥平面AB1E．
（Ⅱ）取AB中点F，连结CF，A1F，先证明A1F⊥AB，由CA=CB可证明CF⊥AB，由CF∩A1F=F，可证明AB⊥面CFA1，从而可证明AB⊥A1C．
（Ⅱ）取AB中点F，连结CF，A1F，先证明A1F⊥AB，由CA=CB可证明CF⊥AB，由CF∩A1F=F，可证明AB⊥面CFA1，从而可证明AB⊥A1C．
解答：
（本题满分12分）
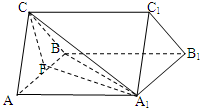
证明：（Ⅰ）连结A1B，使A1B∩AB1=O，连结EO，
因为ABB1A1为平行四边形，所以O为A1B中点，
又因为E为BC中点，所以EO∥A1C，
又因为EO?平面AB1E，
A1C?平面AB1E，
所以，A1C∥平面AB1E；…（6分）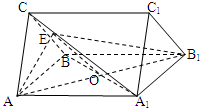
（Ⅱ）取AB中点F，连结CF，A1F，
∵AB=AA1，∠BAA1=60°，∴△BAA1是正三角形，
∴A1F⊥AB，∵CA=CB，∴CF⊥AB，
∵CF∩A1F=F，∴AB⊥面CFA1，
∴AB⊥A1C． …（12分）
（本题满分12分）证明：（Ⅰ）连结A1B，使A1B∩AB1=O，连结EO，
因为ABB1A1为平行四边形，所以O为A1B中点，
又因为E为BC中点，所以EO∥A1C，
又因为EO?平面AB1E，
A1C?平面AB1E，
所以，A1C∥平面AB1E；…（6分）
（Ⅱ）取AB中点F，连结CF，A1F，
∵AB=AA1，∠BAA1=60°，∴△BAA1是正三角形，
∴A1F⊥AB，∵CA=CB，∴CF⊥AB，
∵CF∩A1F=F，∴AB⊥面CFA1，
∴AB⊥A1C． …（12分）
点评：本题主要考查了直线与平面平行的判定，空间中直线与直线之间的位置关系，考查了空间想象能力，属于基本知识的考查．
练习册系列答案
相关题目