题目内容
已知函数f(x)=
x3+bx2+cx,g(x)=mx2+
x-9
(1)当a=3,b=c=0时,若存在过点(1,0)的直线与曲线y=f(x)和y=g(x)都相切,求实数m的值;
(2)当b>a>0时,函数y=f(x)在R上单调递增,求
的最小值.
| a |
| 3 |
| 15 |
| 4 |
(1)当a=3,b=c=0时,若存在过点(1,0)的直线与曲线y=f(x)和y=g(x)都相切,求实数m的值;
(2)当b>a>0时,函数y=f(x)在R上单调递增,求
| a+b+c |
| b-a |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的概念及应用,导数的综合应用,不等式的解法及应用
分析:(1)分别求出f(x),g(x)的导数,设出切点,求得切线的斜率,运用两点的斜率公式和点在曲线上的条件,解方程即可得到;
(2)由题意得f'(x)=ax2+bx+c在R上恒大于或等于0,得a>0,△=b2-4ac≤0,将此代入求
,将式子进行放缩,以
为单位建立函数关系式,最后构造出运用基本不等式的模型使问题得到解决.
(2)由题意得f'(x)=ax2+bx+c在R上恒大于或等于0,得a>0,△=b2-4ac≤0,将此代入求
| a+b+c |
| b-a |
| b |
| a |
解答:
解:(1)当a=3,b=c=0时,f(x)=x3,f′(x)=3x2,
g(x)的导数为g′(x)=2mx+
,
设过点(1,0)的切线与y=f(x)的切点为(e,f),
与y=g(x)的切点为(s,t),
则3e2=2ms+
,
由e3=f,3e2=
=
,解得e=0或
,
则切线的方程为y=0或y=
(x-1).
若e=0,则ms=-
,且t=ms2+
s-9,
=0,
解得t=0,s=
,m=-
;
若e=
,则ms=
,且t=ms2+154s-9,
=
,
解得s=-
,m=-1.
综上可得,m=-
或m=-1.
(2)由题意f'(x)=ax2+bx+c≥0在R上恒成立,
则a>0,△=b2-4ac≤0即有ac≥
b2,
即有
=
≥
=
,
令t=
(t>1),
≥
=
(t-1+
+6)≥
×(2
+6)=3.
(当且仅当t=4,即b=c=4a时取“=”)
即有
的最小值为3.
g(x)的导数为g′(x)=2mx+
| 15 |
| 4 |
设过点(1,0)的切线与y=f(x)的切点为(e,f),
与y=g(x)的切点为(s,t),
则3e2=2ms+
| 15 |
| 4 |
由e3=f,3e2=
| f |
| e-1 |
| e3 |
| e-1 |
| 3 |
| 2 |
则切线的方程为y=0或y=
| 27 |
| 4 |
若e=0,则ms=-
| 15 |
| 8 |
| 15 |
| 4 |
| t |
| s-1 |
解得t=0,s=
| 24 |
| 5 |
| 25 |
| 64 |
若e=
| 3 |
| 2 |
| 3 |
| 2 |
| t |
| s-1 |
| 27 |
| 4 |
解得s=-
| 3 |
| 2 |
综上可得,m=-
| 25 |
| 64 |
(2)由题意f'(x)=ax2+bx+c≥0在R上恒成立,
则a>0,△=b2-4ac≤0即有ac≥
| 1 |
| 4 |
即有
| a+b+c |
| b-a |
| a2+ab+ac |
| ab-a2 |
a2+ab+
| ||
| ab-a2 |
4+
| ||||
4(
|
令t=
| b |
| a |
| a+b+c |
| b-a |
| 4+4t+t2 |
| 4(t-1) |
| 1 |
| 4 |
| 9 |
| t-1 |
| 1 |
| 4 |
| 9 |
(当且仅当t=4,即b=c=4a时取“=”)
即有
| a+b+c |
| b-a |
点评:本题考查导数的几何意义:函数在某点的导数即为曲线在该点处的切线的斜率,同时考查导数的运用:判断单调性,正确设出切点和求出导数,运用两点的斜率公式以及运用基本不等式是解题的关键.

练习册系列答案
相关题目
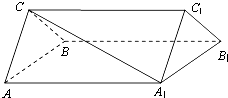 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,E为BC中点
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,E为BC中点