题目内容
已知等差数列{an}的公差不为零，a1=25，且a1，a11，a13成等比数列，求数列{an}的通项公式．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：设等差数列{an}的公差为d（d≠0），依题意，可求得d=-2，从而可得数列{an}的通项公式．
解答：
解：设等差数列{an}的公差为d（d≠0），依题意（a1+10d）2=a1•（a1+12d），
整理得：2a1+25d=0，又a1=25，
所以，d=-2，
所以an=25+（n-1）×（-2）=27-2n．
整理得：2a1+25d=0，又a1=25，
所以，d=-2，
所以an=25+（n-1）×（-2）=27-2n．
点评：本题着重考查等比数列的通项公式与等差数列的性质，考查学生的计算能力，属于中档题．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
定义在R上的奇函数f（x），当x≥0时，f（x）=
，则函数F（x）=f（x）-
的所有零点之和为（ ）
|
| 1 |
| π |
A、
| ||
B、
| ||
C、
| ||
D、
|
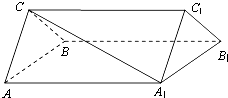如图，三棱柱ABC-A1B1C1中，CA=CB，AB=AA1，∠BAA1=60°，E为BC中点