题目内容
已知函数f(x)=x2+ax+3-a,其中x∈[-2,2].
(1)当a∈R时,讨论它的单调性;
(2)若f(x)≥12-4a恒成立,求a的取值范围.
(1)当a∈R时,讨论它的单调性;
(2)若f(x)≥12-4a恒成立,求a的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)先求出函数的对称轴,对对称轴的范围进行讨论,从而得到函数的单调性;
(2)根据函数的单调性,结合二次函数的图象及性质,得到不等式组,解出即可.
(2)根据函数的单调性,结合二次函数的图象及性质,得到不等式组,解出即可.
解答:
解:(1)f(x)=x2+ax+3-a,对称轴方程为x=-
,
下面分三种情况讨论:
当-
≤-2得a≥4,f(x)单调增区间为[-2,2];
当-
≥2得a≤-4,f(x)单调减区间为[-2,2];
当-4≤a≤4时,f(x)单调增区间为[-2,-
],单调减区间为(-
,2];
(2)方法一:当-
≤-2得a≥4,f(x)单调增区间为[-2,2],f(x)min=f(-2),
当-4≤a≤4时,f(x)单调增区间为[-2,-
],单调减区间为(-
,2],f(x)min=f(-
),
当-
≥2得a≤-4,f(x)单调减区间为[-2,2],f(x)min=f(2),
若x∈[-2,2]时,有f(x)≥12-4a恒成立;
则
⇒a≥5,或
⇒无解,或
⇒无解,
综上可知,a≥5所以,a的取值范围是[5,+∞);
方法二:若x∈[-2,2]时,有f(x)≥12-4a恒成立;
则,f(-2)≥12-4a⇒a≥5,
而当a≥5时,f(x)在[-2,2]上单调递增;所以,x∈[-2,2],f(x)min=f(-2),
若x∈[-2,2]时,有f(x)≥12-4a恒成立,
则
⇒a≥5,
所以,a的取值范围是[5,+∞).
| a |
| 2 |
下面分三种情况讨论:
当-
| a |
| 2 |
当-
| a |
| 2 |
当-4≤a≤4时,f(x)单调增区间为[-2,-
| a |
| 2 |
| a |
| 2 |
(2)方法一:当-
| a |
| 2 |
当-4≤a≤4时,f(x)单调增区间为[-2,-
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
当-
| a |
| 2 |
若x∈[-2,2]时,有f(x)≥12-4a恒成立;
则
|
|
|
综上可知,a≥5所以,a的取值范围是[5,+∞);
方法二:若x∈[-2,2]时,有f(x)≥12-4a恒成立;
则,f(-2)≥12-4a⇒a≥5,
而当a≥5时,f(x)在[-2,2]上单调递增;所以,x∈[-2,2],f(x)min=f(-2),
若x∈[-2,2]时,有f(x)≥12-4a恒成立,
则
|
所以,a的取值范围是[5,+∞).
点评:本题考查了二次函数的性质,函数的单调性,求参数的范围问题,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个四面体的顶点在空间直角坐系O-xyz中的坐标分别是(1,0,0),(0,0,1),(0,1,0),(1,1,1),画该四面体三视图中的正视图时,以zOy平面为投影面,则得到的正视图可为( )
A、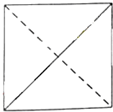 |
B、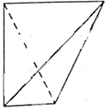 |
C、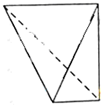 |
D、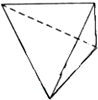 |
圆x2+y2-2x-2y+1=0和圆x2+y2-8x-10y+25=0的位置关系是( )
| A、相交 | B、外切 | C、内切 | D、相离 |