题目内容
23.已知向量
=(1,
),
=(x,1)其中a∈R,函数f(x)=
•
(Ⅰ)试求函数f(x)的解析式;
(Ⅱ)试求当a=1时,函数f(log2x)在区间(1,+∞)上的最小值;
(Ⅲ)若函数f(x)在区间[1,+∞)上为增函数,试求实数a的取值范围.
| m |
| a |
| x |
| n |
| m |
| n |
(Ⅰ)试求函数f(x)的解析式;
(Ⅱ)试求当a=1时,函数f(log2x)在区间(1,+∞)上的最小值;
(Ⅲ)若函数f(x)在区间[1,+∞)上为增函数,试求实数a的取值范围.
考点:平面向量数量积的运算,函数解析式的求解及常用方法,函数单调性的判断与证明,函数的最值及其几何意义
专题:函数的性质及应用,平面向量及应用
分析:(I)利用数量积运算即可得出.
(II)利用对数函数的单调性与基本不等式的性质即可得出.
(III)利用导数研究函数的单调性即可得出.
(II)利用对数函数的单调性与基本不等式的性质即可得出.
(III)利用导数研究函数的单调性即可得出.
解答:
解:(Ⅰ)函数f(x)=
•
=x+
,(x≠0).
(Ⅱ)当a=1时,f(x)=x+
.
∵x∈(1,+∞)时,log2x>0,
∴f(log2x)=log2x+
≥2
=2,
当且仅当log2x=
即x=2时,f(log2x)取最小值2.
( III)∵函数f(x)在区间[1,+∞)上为增函数,
∴f′(x)=1-
≥0在区间[1,+∞)上恒成立,
∴a≤x2在区间[1,+∞)上恒成立,
∴a≤1.
| m |
| n |
| a |
| x |
(Ⅱ)当a=1时,f(x)=x+
| 1 |
| x |
∵x∈(1,+∞)时,log2x>0,
∴f(log2x)=log2x+
| 1 |
| log2x |
log2x•
|
当且仅当log2x=
| 1 |
| log2x |
( III)∵函数f(x)在区间[1,+∞)上为增函数,
∴f′(x)=1-
| a |
| x2 |
∴a≤x2在区间[1,+∞)上恒成立,
∴a≤1.
点评:本题考查了数量积运算、对数函数的单调性与基本不等式的性质、利用导数研究函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
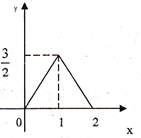
图中的图象所表示的函数的解析式为( )

A、y=
| ||
B、y=
| ||
C、y=
| ||
| D、2-|x-1|(0≤x≤2) |
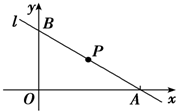 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△ABO的面积的最小值及此时直线l的方程.
已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,求△ABO的面积的最小值及此时直线l的方程.