题目内容
已知函数f(x)=2x|2x-a|+b.
(Ⅰ) 当a=1,b=0时,判断函数f(x)的奇偶性,并说明理由;
(Ⅱ) 当a=b=4时,若f(x)=5,求x的值;
(Ⅲ) 若b<-4,且b为常数,对于任意x∈(0,2],都有f(log2x)<0成立,求a的取值范围.
(Ⅰ) 当a=1,b=0时,判断函数f(x)的奇偶性,并说明理由;
(Ⅱ) 当a=b=4时,若f(x)=5,求x的值;
(Ⅲ) 若b<-4,且b为常数,对于任意x∈(0,2],都有f(log2x)<0成立,求a的取值范围.
考点:奇偶性与单调性的综合,函数奇偶性的判断
专题:函数的性质及应用
分析:(Ⅰ) 当a=1,b=0时,根据函数奇偶性的定义即可判断函数f(x)的奇偶性;
(Ⅱ) 当a=b=4时,若f(x)=5,解方程即可求x的值;
(Ⅲ) 根据不等式的解法,即可得到结论.
(Ⅱ) 当a=b=4时,若f(x)=5,解方程即可求x的值;
(Ⅲ) 根据不等式的解法,即可得到结论.
解答:
解:(Ⅰ) 当a=1,b=0时,f(x)=2x|2x-1|.
∵f(1)=2,f(-1)=
×
=
,
∴f(-1)≠-f(1),f(-1)≠f(1),
故函数f(x)为非奇非偶函数;
(Ⅱ) 当a=b=4时,若f(x)=5,
则f(x)=2x|2x-4|+4=5.
即2x|2x-4|=1.
若2x-4≥0,即x≥2,则等价为2x(2x-4)-1=0.
即(2x)2-4•2x-1=0
解得2x=2+
,即x=log2(2+
);
若2x-4<0,即x<2,则等价为-2x(2x-4)-1=0.
即(2x)2-4•2x+1=0
解得2x=2-
,
即x=log2(2-
),
综上x=log2(2-
)或x=log2(2+
);
(Ⅲ) 不等式等价于x+
<a<x-
,
根据函数的单调性,x+
的最大值为2+
,x-
的最小值为2-
,
所以 2+
<a<2-
.
∵f(1)=2,f(-1)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴f(-1)≠-f(1),f(-1)≠f(1),
故函数f(x)为非奇非偶函数;
(Ⅱ) 当a=b=4时,若f(x)=5,
则f(x)=2x|2x-4|+4=5.
即2x|2x-4|=1.
若2x-4≥0,即x≥2,则等价为2x(2x-4)-1=0.
即(2x)2-4•2x-1=0
解得2x=2+
| 5 |
| 5 |
若2x-4<0,即x<2,则等价为-2x(2x-4)-1=0.
即(2x)2-4•2x+1=0
解得2x=2-
| 3 |
即x=log2(2-
| 3 |
综上x=log2(2-
| 3 |
| 5 |
(Ⅲ) 不等式等价于x+
| b |
| x |
| b |
| x |
根据函数的单调性,x+
| b |
| x |
| b |
| 2 |
| b |
| x |
| b |
| 2 |
所以 2+
| b |
| 2 |
| b |
| 2 |
点评:本题主要考查函数奇偶性的定义以及对数方程的解法是解决本题的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
方程x2+(m-3)x+m=0有两个正实数根,则m的取值范围是( )
| A、0≤m<1 |
| B、0<m<1 |
| C、0<m≤1 |
| D、0≤m≤1 |
数列1,3,6,10,…的一个通项公式是( )
| A、an=n2-n+1 | ||
B、an=
| ||
C、an=
| ||
| D、an=n2+1 |
若a>0且a≠1,那么函数y=ax与y=logax的图象关于( )
| A、原点对称 | B、直线y=x对称 |
| C、x轴对称 | D、y轴对称 |
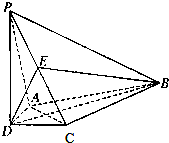 如图,在四棱锥P-ABCD中,PD垂直平面ABCD,AD=CD,DB平分角ADC,E为PC的重点.
如图,在四棱锥P-ABCD中,PD垂直平面ABCD,AD=CD,DB平分角ADC,E为PC的重点.