题目内容
 欲修建一横断面为等腰梯形(如图)的水渠,为降低成本必须尽量减少水与渠壁的接触面,若水渠横断面面积设计为定值S,渠深h,则水渠壁的倾角α(0°<α<90°)应为多大时,方能使修建成本最低?
欲修建一横断面为等腰梯形(如图)的水渠,为降低成本必须尽量减少水与渠壁的接触面,若水渠横断面面积设计为定值S,渠深h,则水渠壁的倾角α(0°<α<90°)应为多大时,方能使修建成本最低?考点:导数在最大值、最小值问题中的应用
专题:函数的性质及应用,直线与圆
分析:作BE⊥DC于E,令y=AD+DC+BC,由已知可得y=
+
(0°<α<90°),令u=
,求出u取最小值时α的大小,可得结论.
| S |
| h |
| h(2-cosα) |
| sinα |
| 2-cosα |
| sinα |
解答:
解:作BE⊥DC于E,

在Rt△BEC中,BC=
,CE=hcotα,
又AB-CD=2CE=2hcotα,AB+CD=
,
故CD=
-hcotα.
设y=AD+DC+BC,
则y=
-hcotα+
=
+
(0°<α<90°),
由于S与h是常量,欲使y最小,只需u=
取最小值,
u可看作(0,2)与(-sinα,cosα)两点连线的斜率,
由于α∈(0°,90°),
点(-sinα,cosα)在曲线x2+y2=1(-1<x<0,0<y<1)上运动,
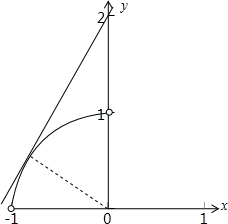
当过(0,2)的直线与曲线相切时,直线斜率最小,
此时切点为(-
,
),
则有sinα=
,且cosα=
,
那么α=60°,
故当α=60°时,修建成本最低.

在Rt△BEC中,BC=
| h |
| sinα |
又AB-CD=2CE=2hcotα,AB+CD=
| 2S |
| h |
故CD=
| S |
| h |
设y=AD+DC+BC,
则y=
| S |
| h |
| 2h |
| sinα |
| S |
| h |
| h(2-cosα) |
| sinα |
由于S与h是常量,欲使y最小,只需u=
| 2-cosα |
| sinα |
u可看作(0,2)与(-sinα,cosα)两点连线的斜率,
由于α∈(0°,90°),
点(-sinα,cosα)在曲线x2+y2=1(-1<x<0,0<y<1)上运动,

当过(0,2)的直线与曲线相切时,直线斜率最小,
此时切点为(-
| ||
| 2 |
| 1 |
| 2 |
则有sinα=
| ||
| 2 |
| 1 |
| 2 |
那么α=60°,
故当α=60°时,修建成本最低.
点评:本题考查的知识点是函数的最值,直线与圆的位置关系,其中求出水与渠壁的接触面y的解析式,将实际问题转化为函数问题,是解答的关键.

练习册系列答案
相关题目