题目内容
9.一个几何体的三视图如图所示,其体积为( )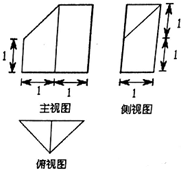
| A. | $\frac{11}{6}$ | B. | $\frac{11}{6}\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
分析 画出三视图对应的几何体的图形,判断几何体的形状,利用三视图的数据求解几何体的体积即可.
解答 解:该几何体是一个直三棱柱截去一个小三棱锥,如图所示,则其体积为:$V=\frac{1}{2}×2×1×2-\frac{1}{3}×\frac{1}{2}×1×1×1=\frac{11}{6}$.
故选:A.
点评 本题考查三视图与几何体的关系,几何体的体积的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
20.若方程x2+y2-x+y+m=0表示一个圆,则二次函数y=-x2+mx+m在(-∞,$\frac{1}{4}$)的单调性是( )
| A. | 增函数 | B. | 减函数 | C. | 先减后增 | D. | 先增后减 |
17.已知向量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-1,2),若(m$\overrightarrow{a}$+n$\overrightarrow{b}$)∥($\overrightarrow{a}$-2$\overrightarrow{b}$),则$\frac{m}{n}$等于( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
14.若a=ln2,b=${5^{-\frac{1}{2}}}$,c=$\frac{1}{4}\int_0^π$sinxdx,则a,b,c的大小关系( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | b<c<a |
1.一个几何体的三视图如图,则这个几何体的表面积是( )
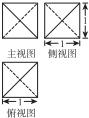

| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{3}$ | D. | $2\sqrt{6}$ |
18.已知x>0,y>0,lg2x+lg8y=lg2,则$\frac{1}{x}+\frac{2}{y}$的最小值是( )
| A. | $7+2\sqrt{6}$ | B. | $4+\sqrt{3}$ | C. | $7+\sqrt{6}$ | D. | $4+2\sqrt{3}$ |
19.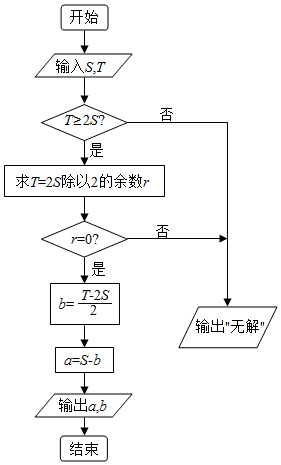 《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )
《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )
 《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )
《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )| A. | S=40,T=120 | B. | S=40,T=126 | C. | S=42,T=126 | D. | S=42,T=130 |