一个几何体的三视图如图.则这个几何体的表面积是( )A．$\sqrt{3}$B．$\sqrt{6}$C．$2\sqrt{3}$D．$2\sqrt{6}$ 题目和参考答案——青夏教育精英家教网—

题目内容

1．一个几何体的三视图如图，则这个几何体的表面积是（　　）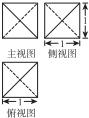

A．

$\sqrt{3}$

B．

$\sqrt{6}$

C．

$2\sqrt{3}$

D．

$2\sqrt{6}$

分析画出三视图复原的几何体，判断几何体的形状，然后求解几何体的表面积．

解答解：由三视图可知，几何体是正方体内的三棱锥D-BA₁C₁，正方体的棱长为：1，面对角线长度为：$\sqrt{2}$，就是几何体的棱长为：$\sqrt{2}$，几何体是正四面体，所以S=4×$\frac{\sqrt{3}}{4}×（\sqrt{2}）^{2}$=2$\sqrt{3}$．

故选：C．

点评本题考查三视图对应的几何体的形状，几何体的表面积的求法，考查计算能力．

练习册系列答案

12．求下列方程的解集：
（1）sin$\frac{x}{2}$-cos$\frac{x}{2}$=1；
（2）sinx-$\sqrt{3}$cosx=$\sqrt{2}$；
（3）$\sqrt{2}$sin2x+$\sqrt{2}$cos2x-1=0；
（4）sinx=2sin（$\frac{π}{3}$-x）．

9．一个几何体的三视图如图所示，其体积为（　　）

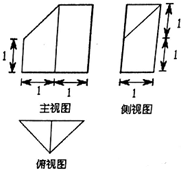
A．

$\frac{11}{6}$

B．

$\frac{11}{6}\sqrt{3}$

16．下面几种推理过程是演绎推理的是（　　）

	A．	某校高三有8个班，1班有51人，2班有53人，由此推断各班人数都超过50人
	B．	由三角形的性质，推测空间四面体的性质
	C．	在数列{a_n}中，a₁=1，a_n+1=$\frac{{a}_{n}}{1+{a}_{n}}$（n=1，2，3），由此归纳出{a_n}的通项公式
	D．	三角函数都是周期函数，tanα是三角函数，因此tanα是周期函数

6．根据定积分的几何意义，计算${∫}_{0}^{3}$$\sqrt{9-{x}^{2}}$dx=$\frac{9π}{4}$．

13．在某次联考数学测试中，学生成绩ξ服从正态分布（100，σ²）（σ＞0），若ξ在（80，120）内的概率为0.8，则落在（0，80）内的概率为0.1．

10．执行如图所示的程序框图，输出的n为（　　）

11．

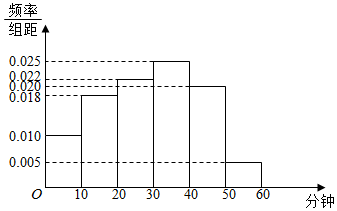某中学为研究学生的身体素质与课外体育锻炼时间的关系，对该校200名学生的课外体育锻炼平均每天运动的时间（单位：分钟）进行调查，将收集到的数据分成[0，10），[10，20），[20，30），[30，40），[40，50），[50，60）六组，并作出频率分布直方图（如图）．将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”．
（1）请根据直方图中的数据填写下面的2×2列联表，并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关？

	课外体育不达标	课外体育达标	合计
男	60	30	90
女	90	20	110
合计	150	50	200

（2）现从课外体育达标学生中按分层抽样抽取5人，再从这5名学生中随机抽取2人参加体育知识问卷调查，求抽取的这2人课外锻炼时间都在[40，50）内的概率．
附参考公式与数据：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$

P（K²≥k₀）	0.10	0.05	0.010	0.005	0.001
k₀	2.706	3.841	6.635	7.879	10.828

试题分类