题目内容

20．若方程x2+y2-x+y+m=0表示一个圆，则二次函数y=-x2+mx+m在（-∞，$\frac{1}{4}$）的单调性是（　　）
A．增函数B．减函数C．先减后增D．先增后减

分析 根据方程x2+y2-x+y+m=0表示一个圆求出m的取值范围，再根据二次函数y=-x2+mx+m的图象与性质，即可得出结论．

解答 解：∵方程x2+y2-x+y+m=0表示一个圆，
∴（-1）2+12-4m＞0，
∴m＜$\frac{1}{2}$；
又二次函数y=-x2+mx+m的图象开口向下，对称轴为x=$\frac{m}{2}$＜$\frac{1}{4}$，
∴函数y在（-∞，$\frac{1}{4}$）上先增后减．
故选：D．

点评 本题考查了二元二次方程表示圆的条件与一元二次函数的图象与性质的应用问题，是基础题目．

练习册系列答案
相关题目
10．若双曲线mx2+2y2=2的虚轴长为2，则该双曲线的焦距为（　　）
A．$\sqrt{2}$B．2$\sqrt{2}$C．$\sqrt{5}$D．2$\sqrt{5}$
11．已知x，y满足条件$\left\{\begin{array}{l}{x-2≤0}\\{x-2y≤0}\\{x+2y-8≤0}\end{array}\right.$，若z=2x+y的最大值为（　　）
A．9B．8C．7D．6
8．已知函数f（x）=|（ax-1）（x-1）|（a∈R）．
（1）当a=$\frac{1}{3}$时，求函数f（x）的单调区间；
（2）当a＞1时，若函数g（x）=f（x）-|x-a|至少有三个零点，求a的取值范围；
（3）当0≤a≤1时，若对任意的x∈[0，2]，都有m≥f（x）恒成立，求m的取值范围．
15．求值|log35-2|+log925+（$\frac{1}{16}$）${\;}^{-\frac{1}{4}}$-e0=3．
5．函数y=$\frac{\sqrt{lg（{x}^{2}-3）}}{x-2}$的定义域为（-∞，-2]∪（2，+∞）．
12．求下列方程的解集：
（1）sin$\frac{x}{2}$-cos$\frac{x}{2}$=1；
（2）sinx-$\sqrt{3}$cosx=$\sqrt{2}$；
（3）$\sqrt{2}$sin2x+$\sqrt{2}$cos2x-1=0；
（4）sinx=2sin（$\frac{π}{3}$-x）．
9．一个几何体的三视图如图所示，其体积为（　　）
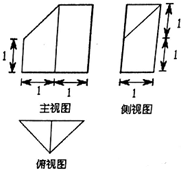
A．$\frac{11}{6}$B．$\frac{11}{6}\sqrt{3}$C．$\frac{3}{2}$D．$\frac{1}{2}$
10．执行如图所示的程序框图，输出的n为（　　）
A．2B．3C．4D．5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网