题目内容
19.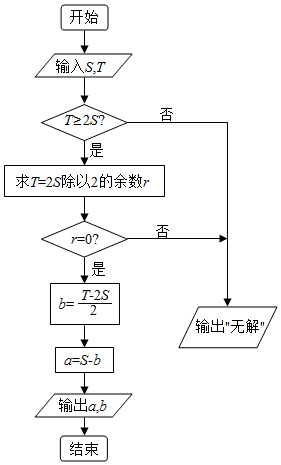 《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )
《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输出的a,b分别为17,23,则输入的S,T分别为( )| A. | S=40,T=120 | B. | S=40,T=126 | C. | S=42,T=126 | D. | S=42,T=130 |
分析 模拟程序的运行,可得程序框图的功能是输入S,T的值,当T≥2S,且T=2S能被2整除时,计算b=$\frac{T-2S}{2}$,a=S-b的值,由输出的a,b分别为17,23,即可计算得解.
解答 解:模拟程序的运行,可得程序框图的功能是输入S,T的值,当T≥2S,且T=2S能被2整除时,计算b=$\frac{T-2S}{2}$,a=S-b的值,
若输出的a,b分别为17,23,
则:17=S-23,解得:S=40,
由b=$\frac{T-2S}{2}$,可得:23=$\frac{T-2×40}{2}$,解得:T=126.
故选:B.
点评 本题主要考查了算法和程序框图的应用,模拟程序的运行,正确得到程序框图的功能是解题的关键,属于基础题.

练习册系列答案
相关题目
9.一个几何体的三视图如图所示,其体积为( )
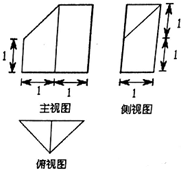

| A. | $\frac{11}{6}$ | B. | $\frac{11}{6}\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
10.执行如图所示的程序框图,输出的n为( )


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.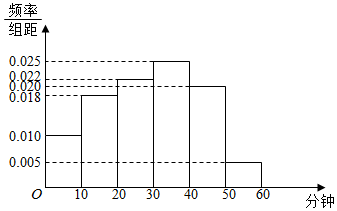 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
(1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
(2)现从课外体育达标学生中按分层抽样抽取5人,再从这5名学生中随机抽取2人参加体育知识问卷调查,求抽取的这2人课外锻炼时间都在[40,50)内的概率.
附参考公式与数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.(1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | 60 | 30 | 90 |
| 女 | 90 | 20 | 110 |
| 合计 | 150 | 50 | 200 |
附参考公式与数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |