题目内容

19．圆Γ的圆周上六个点将圆周等分，经过这6个点中任意两点做圆的弦，在所做的这些弦中任意取出两条，则这两条弦有公共点的概率为$\frac{5}{7}$．

分析 圆Г的圆周上六个点将圆周等分，设这六个点分别为A，B，C，D，C，E，F，先列举出所有的弦，根据排列组合，再找到满足条件的基本事件，根据概率公式计算即可．据排列组合，再找到满足条件的基本事件，根据概率公式计算即可．

解答 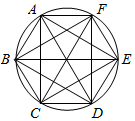解：圆Г的圆周上六个点将圆周等分，设这六个点分别为A，B，C，D，C，E，F，从这六点中的任意两点的连线共有AB，AC，AD，AE，AF，BC，BD，BE，BF，CD，CE，CF，DE，DF，EF，共有15条，所做的这些弦中任意取出两条共有C152=105种，
其中这两条弦有有公共点，第一类，每个顶点处都有5条线．任意选2条都有交点，6×C52=60种，
第二类，正六边形内部，每一个交点处都有2条弦相交，共有15种，
所以这两条弦有公共点的有60+15=75种，
故这两条弦有公共点的概率为$\frac{75}{105}$=$\frac{5}{7}$，
故答案为：$\frac{5}{7}$

点评 本题考查概率的求法，涉及到直线、组合、概率等知识，解题时要注意列举法的合理运用，属于中档题．

练习册系列答案
相关题目
9．若某程序框图如图所示，则该程序运行后输出的值等于5
10．若双曲线mx2+2y2=2的虚轴长为2，则该双曲线的焦距为（　　）
A．$\sqrt{2}$B．2$\sqrt{2}$C．$\sqrt{5}$D．2$\sqrt{5}$
7．已知x，y满足条件$\left\{\begin{array}{l}{x-\frac{1}{2}y+1≥0}\\{x+y≤2}\\{x-2y≤2}\end{array}\right.$，若z=mx+y取得最大值的最优解不唯一，则实数m的值为（　　）
A．1或-$\frac{1}{2}$B．1或-2C．-1或-2D．-2或-$\frac{1}{2}$
14．已知a，b为非零向量，则下列命题中真命题的个数为（　　）
①若|a|+|b|=|a+b|，则a与b方向相同；
②若|a|+|b|=|a-b|，则a与b方向相反；
③若|a|+|b|=|a-b|，则a与b有相等的模；
④若|a|-|b|=|a-b|，则a与b方向相同．
A．0B．1C．2D．3
4．如图所示，半径为4的圆中有一个小狗图案，在圆中随机撒一粒豆子，它落在小狗图案内的概率是$\frac{1}{3}$，则小狗图案的面积是（　　）
A．$\frac{π}{3}$B．$\frac{4π}{3}$C．$\frac{8π}{3}$D．$\frac{16π}{3}$
11．已知x，y满足条件$\left\{\begin{array}{l}{x-2≤0}\\{x-2y≤0}\\{x+2y-8≤0}\end{array}\right.$，若z=2x+y的最大值为（　　）
A．9B．8C．7D．6
8．已知函数f（x）=|（ax-1）（x-1）|（a∈R）．
（1）当a=$\frac{1}{3}$时，求函数f（x）的单调区间；
（2）当a＞1时，若函数g（x）=f（x）-|x-a|至少有三个零点，求a的取值范围；
（3）当0≤a≤1时，若对任意的x∈[0，2]，都有m≥f（x）恒成立，求m的取值范围．
9．一个几何体的三视图如图所示，其体积为（　　）
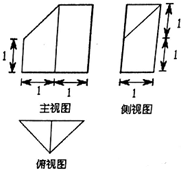
A．$\frac{11}{6}$B．$\frac{11}{6}\sqrt{3}$C．$\frac{3}{2}$D．$\frac{1}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网