题目内容
12.已知f(x)=|x-2|+|x+2|.(1)求不等式f(x)≥6的解集;
(2)若不等式f(x)<a+x的解集不为∅,求a的取值范围.
分析 (1)通过讨论x的范围求出不等式的解集即可;(2)由题知g(x)<a的解集不为空集,即g(x)min<a成立,求出g(x)的最小值,从而求出a的范围即可.
解答 解:(1)原不等式等价于
①$\left\{\begin{array}{l}{x<-2}\\{2-x-(x+2)=-2x≥6}\end{array}\right.$,解得:x≤-3,
②$\left\{\begin{array}{l}{-2≤x≤2}\\{2-x+x+2=4≥6}\end{array}\right.$?,解得:x=∅,
?③$\left\{\begin{array}{l}{x>2}\\{x-2+x+2=2x≥6}\end{array}\right.$,解得:x≥3,
∴原不等式的解集为(-∞,-3]∪[3,+∞);
(2)令g(x)=f(x)-x,则由题知g(x)<a的解集不为空集,
即g(x)min<a成立,
又g(x)=$\left\{\begin{array}{l}{-3x,x<-2}\\{4-x,-2≤x≤2}\\{x,x>2}\end{array}\right.$,
故g(x)的最小值是2,即a>2,
∴a的取值范围为:(2,+∞).
点评 本题考查了解绝对值不等式问题,考查函数的最值问题,是一道中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
20.函数f(x)的定义域为R,且满足f(1)=2,f′(x)<1,则不等式f(x)<x+1的解集为( )
| A. | (1,+∞) | B. | (-∞,1) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
7.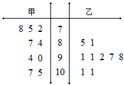 某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )
某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )
 某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )
某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )| A. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲2>s乙2 | B. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲2<s乙2 | ||
| C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲2>s乙2 | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲2<s乙2 |
17.设a,b,c为非零实数,则x=$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{c}{|c|}$+$\frac{{|{abc}|}}{abc}$的所有值所组成的集合为( )
| A. | {0,4} | B. | {-4,0} | C. | {-4,0,4} | D. | {0} |
4.已知f(x)是定义在R上的偶函数,它在[0,+∞)上递增,那么一定有( )
| A. | $f(\frac{3}{4})<f({a^2}-a+1)$ | B. | $f(\frac{3}{4})≤f({a^2}-a+1)$ | C. | $f(\frac{3}{4})>f({a^2}-a+1)$ | D. | $f(\frac{3}{4})≥f({a^2}-a+1)$ |
1.已知圆x2+y2-4x+2y=0,则过圆内一点E(1,0)的最短弦长为( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{5}$ |
2.若变量x,y满足约束条件$\left\{\begin{array}{l}x+2y-2≥0\\ 2x+y-4≤0\\ 4x-y+1≥0\end{array}\right.$,则目标函数z=y-2x的最大值是( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | 3 | D. | $\frac{5}{2}$ |