题目内容
10.在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°(1)若PB=1,求PA;
(2)若∠APB=120°,设∠PBA=α,求tanα的值.
分析 (1)由已知得∠PBC=60°,可得∠PBA=30°,在△PBA中,由余弦定理即可得出.
(2)已知得∠PCB=α,PB=2sinα,在△PBA中,由正弦定理得$\frac{2\sqrt{3}}{sin120°}=\frac{2sinα}{sin(60°-α)}$,化简整理即可得出.
解答  解:(1)由已知得∠PBC=60°,∴∠PBA=30°,
解:(1)由已知得∠PBC=60°,∴∠PBA=30°,
在△PBA中,由余弦定理得PA=$\sqrt{12+1-2×2\sqrt{3}×1×\frac{\sqrt{3}}{2}}$=$\sqrt{7}$.
(2)由已知得∠PCB=α,PB=2sinα,
在△PBA中,由正弦定理得$\frac{2\sqrt{3}}{sin120°}=\frac{2sinα}{sin(60°-α)}$,化简得3cosα=2$\sqrt{3}$sinα,
∴tanα=$\frac{\sqrt{3}}{2}$.
点评 本题考查了正弦定理余弦定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.若集合A={x|x>-1},下列关系式中成立的为( )
| A. | 0⊆A | B. | {0}∈A | C. | ∅∈A | D. | {0}⊆A |
15.曲线y=sin$\frac{πx}{2}$与y=x3围成的图形的面积是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{π}-\frac{1}{4}$ | D. | $\frac{4}{π}-\frac{1}{2}$ |
9.直线x+y=$\sqrt{3}$a与圆x2+y2=a2+(a-1)2相交于点A、B,点O是坐标原点,若△AOB是正三角形,则实数a=( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
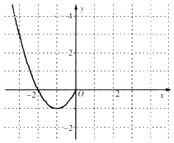 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x. 某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如图:
某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如图: