题目内容
20. 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.(I)求函数f(x)的解析式
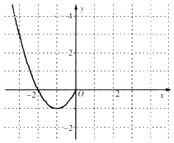
(II)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的单调区间和值域.
分析 (Ⅰ)利用函数的奇偶性,结合已知条件,求解函数的解析式即可.
(Ⅱ)画出函数的图象,利用函数的图象,求解函数的单调区间与函数的值域即可.
解答 解:(Ⅰ)当x>0时,-x<0∴f(-x)=(-x)2-2x=x2-2x
又∵函数f(x)是定义在R上的偶函数∴f(x)=x2-2x
∴$f(x)=\left\{{\begin{array}{l}{{x^2}+2x,(x≤0)}\\{{x^2}-2x,(x>0)}\end{array}}\right.$;
(Ⅱ)如图所示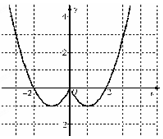
由图象知函数f(x)的增区间为(-1,0)和(1,+∞);减区间为(-∞,-1)和(0,1)
函数f(x)的值域为[-1,+∞).
点评 本题考查函数的图象与函数的解析式的求法,函数的值域与函数的单调性的判断,考查计算能力.

练习册系列答案
相关题目
15.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如表统计数据表:
根据上表可得回归直线方程$\stackrel{∧}{y}$=a+0.76x,据此估计,若该社区一户家庭年支出为11.8万元,则该家庭的年收入为15万元.
| 收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
5.在△ABC中,a,b,c分别为角A,B,C所对的边,若c=4,且C=60°,则ab的最大值为( )
| A. | 4 | B. | 1+$\sqrt{3}$ | C. | 16 | D. | $\frac{1+\sqrt{3}}{2}$ |
12.已知函数f(x)=asinx在点(0,0)处的切线方程为y=2x,则a=( )
| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{1}{2}$ |