题目内容
2.函数$f(x)={(\frac{1}{2})^{2{x^2}-3x+1}}$的增区间是$(-∞,\frac{3}{4}]$.分析 令t=2x2-3x+1,求出其单调性区间,则g(t)=($\frac{1}{2}$)t是单调递减,根据复合函数的单调性可得增区间.
解答 解:函数$f(x)={(\frac{1}{2})^{2{x^2}-3x+1}}$,
令t=2x2-3x+1,
则函数f(x)转化为g(t)=($\frac{1}{2}$)t是单调递减,
函数t=2x2-3x+1,
开口向上,对称轴x=$\frac{3}{4}$,
其单调性区间,单调增区间为:[$\frac{3}{4}$,+∞)单调减区间为(-∞,$\frac{3}{4}$];
根据复合函数的单调性“同增异减”可得函数f(x)的单调增区间为(-∞,$\frac{3}{4}$];
故答案为:$(-∞,\frac{3}{4}]$.
点评 本题考查了复合函数的单调性的求法.属于基础题.

练习册系列答案
相关题目
12.已知函数f(x)=asinx在点(0,0)处的切线方程为y=2x,则a=( )
| A. | 1 | B. | 2 | C. | 4 | D. | $\frac{1}{2}$ |
10.在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°
(1)若PB=1,求PA;
(2)若∠APB=120°,设∠PBA=α,求tanα的值.
(1)若PB=1,求PA;
(2)若∠APB=120°,设∠PBA=α,求tanα的值.
7.函数f(x)=ex(2-|x|)-1的零点个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
14.设向量$\overrightarrow a$,$\overrightarrow b$满足$|\overrightarrow a|=1$,$|\overrightarrow a+\overrightarrow b|=\sqrt{3}$,$\overrightarrow a•(\overrightarrow a+\overrightarrow b)=0$,则$|2\overrightarrow a-\overrightarrow b|$=( )
| A. | 2 | B. | $2\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
11.设抛物线y2=8x的焦点为F,M是抛物线上一点,N(2,2),则|MF|+|MN|的取值范围是( )
| A. | (0,4] | B. | [4,+∞) | C. | (0,2] | D. | [2,+∞) |
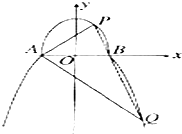 如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.
如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.