题目内容
已知曲线C的极坐标方程是ρ=
cos(θ+
).以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
(t为参数),则直线l与曲线C相交所成的弦的弦长为 .
| 2 |
| π |
| 4 |
|
考点:点的极坐标和直角坐标的互化,参数方程化成普通方程
专题:坐标系和参数方程
分析:把曲线C的极坐标方程展开,再利用
即可化为直角坐标方程,把直线l的方程化为普通方程,利用弦长公式l=2
即可得出.
|
| r2-d2 |
解答:
解:由曲线C的极坐标方程ρ=
cos(θ+
),化为ρ=
(
cosθ-
sinθ),即ρ=cosθ-sinθ,
∴ρ2=ρcosθ-ρsinθ,
∴x2+y2=x-y.
化为(x-
)2+(y+
)2=
.表示圆心为C(
,-
),半径r=
的圆.
直线l的参数方程是:
(t为参数)化为3x+4y+1=0.
∴圆心C到直线l的距离d=
=
.
∴直线l与曲线C相交所成的弦的弦长=2
=
.
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴ρ2=ρcosθ-ρsinθ,
∴x2+y2=x-y.
化为(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
直线l的参数方程是:
|
∴圆心C到直线l的距离d=
|
| ||||
|
| 1 |
| 10 |
∴直线l与曲线C相交所成的弦的弦长=2
| r2-d2 |
| 7 |
| 5 |
点评:本题考查了把圆的极坐标方程化为直角坐标方程、圆的弦长公式、点到直线的距离公式,考查了推理能力和计算能力,属于基础题.

练习册系列答案
相关题目
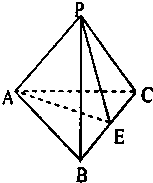 如图所示,点P是平面ABC外一点,且满足PA、PB、PC两两垂直,PE⊥BC,则该图中两两垂直的平面共有( )
如图所示,点P是平面ABC外一点,且满足PA、PB、PC两两垂直,PE⊥BC,则该图中两两垂直的平面共有( )| A、3对 | B、4对 | C、5对 | D、6对 |
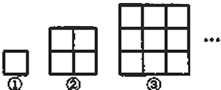 如图图形都是由同样大小的正方形按一定规律组成,第①个图形中有1个正方形,第②个图形中有5个正方形,…,则第⑥个图形中正方形的个数是( )
如图图形都是由同样大小的正方形按一定规律组成,第①个图形中有1个正方形,第②个图形中有5个正方形,…,则第⑥个图形中正方形的个数是( )| A、36 | B、55 | C、70 | D、91 |
有一个几何体的三视图如图所示,这个几何体是一个( )


| A、棱台 | B、棱锥 | C、棱柱 | D、圆台 |
 如图所示,一个空间几何的主视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为
如图所示,一个空间几何的主视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为