题目内容
12．已知（1-2x）9=a0+a1x+a2x2+…+a9x9，则a0+a1+a2+…+a9=-1．分析 令x=1，可得：（1-2）9=a0+a1+a2+…+a9，化简即可得出．
解答 解：令x=1，可得：（1-2）9=a0+a1+a2+…+a9，
则a0+a1+a2+…+a9=（-1）9=-1．
故答案为：-1．
点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
20．已知（x-1）n的二项展开式的奇数项二项式系数和为64，若（x-1）n=a0+a1（x+1）+a2（x+1）2+…+an（x+1）n，则a1等于（ ）
| A． | 192 | B． | 448 | C． | -192 | D． | -448 |
7．在下面给出的四个函数中，既是区间（0，$\frac{π}{2}$）上的增函数，又是以π为周期的偶函数的是（ ）
| A． | y=|sinx| | B． | y=|cosx| | C． | y=sin2x | D． | y=cos2x |
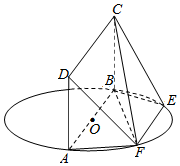如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，矩形ABCD所在平面和圆O所在的平面互相垂直．已知AB=2，EF=1．