题目内容
20.已知(x-1)n的二项展开式的奇数项二项式系数和为64,若(x-1)n=a0+a1(x+1)+a2(x+1)2+…+an(x+1)n,则a1等于( )| A. | 192 | B. | 448 | C. | -192 | D. | -448 |
分析 (x-1)n=(-2+x+1)n=${∁}_{n}^{0}(-2)^{n}$+${∁}_{n}^{1}(-2)^{n-1}(x+1)$+${∁}_{n}^{2}(-2)^{n-2}$(x+1)2+…+${∁}_{n}^{n}(x+1)^{n}$,由于(x-1)n的二项展开式的奇数项二项式系数和为64,可得$64=\frac{{2}^{n}}{2}$,解得n.即可得出.
解答 解:(x-1)n=(-2+x+1)n=${∁}_{n}^{0}(-2)^{n}$+${∁}_{n}^{1}(-2)^{n-1}(x+1)$+${∁}_{n}^{2}(-2)^{n-2}$(x+1)2+…+${∁}_{n}^{n}(x+1)^{n}$=a0+a1(x+1)+a2(x+1)2+…+an(x+1)n,
∵(x-1)n的二项展开式的奇数项二项式系数和为64,∴$64=\frac{{2}^{n}}{2}$,解得n=7.
则a1=${∁}_{7}^{1}(-2)^{6}$=448.
故选:B.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.下列导数运算错误的是( )
| A. | (x-2)′=-2x-1 | B. | (cosx)′=-sinx | C. | (xlnx)′=1+lnx | D. | (2x)′=2xln2 |
11.若sin2α<0且tanαcosα>0,则角α是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
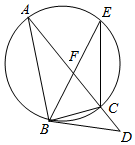 如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D
如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D