题目内容
2.已知数列{an}满足an+2an+1=7×3n-1,且a1=1,则a3=9,通项an=3n-1(用n表示).分析 an+2an+1=7×3n-1,且a1=1,分别令n=1,2,可得a2,a3.由an+2an+1=7×3n-1,变形为:an+1-3n=-$\frac{1}{2}({a}_{n}-{3}^{n-1})$,由a1=1,可得a2=3,同理可得a3=32,依次递推即可得出.
解答 解:∵an+2an+1=7×3n-1,且a1=1,
∴1+2a2=7,a2+2a3=7×3,
解得a2=3,a3=9.
由an+2an+1=7×3n-1,变形为:an+1-3n=-$\frac{1}{2}({a}_{n}-{3}^{n-1})$,
∴由a1=1,可得a2=3,同理可得a3=32,
依次递推可得:an=3n-1.
故答案分别为:9;3n-1.
点评 本题考查了递推关系、数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列导数运算错误的是( )
| A. | (x-2)′=-2x-1 | B. | (cosx)′=-sinx | C. | (xlnx)′=1+lnx | D. | (2x)′=2xln2 |
11.若sin2α<0且tanαcosα>0,则角α是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |

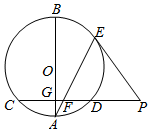 如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G,E是劣弧$\widehat{BD}$上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G,E是劣弧$\widehat{BD}$上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.