题目内容
17．在四面体A-BCD中，AB=AD=CD=2，CB=4，面ABD⊥面CBD，CD⊥BD，则四面体A-BCD的体积为$\frac{2\sqrt{3}}{3}$．分析 过A作AE⊥BD，则AE为棱锥的高，利用勾股定理求出BD，AE，代入体积公式计算即可．
解答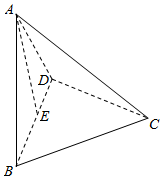 
解：取BD中点E，连结AE．
∵AB=AD，E是BD的中点，
∴AE⊥BD，
∵面ABD⊥面CBD，面ABD∩面CBD=BD，AE?平面ABD，
∴AE⊥平面BCD，
∵CD⊥BD，∴BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=2$\sqrt{3}$．
∴BE=$\frac{1}{2}BD=\sqrt{3}$，
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=1．
∴VA-BCD=$\frac{1}{3}{S}_{△BCD}•AE$=$\frac{1}{3}×\frac{1}{2}×2\sqrt{3}×2×1$=$\frac{2\sqrt{3}}{3}$．
故答案为：$\frac{2\sqrt{3}}{3}$．
点评 本题考查了面面垂直的性质，棱锥的体积计算，属于基础题．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
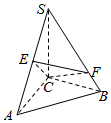直线SC⊥面ABC，AB⊥BC，且AB=BC=1，SA=2，E为SA中点，F为点C在线BS上的射影．