题目内容
4.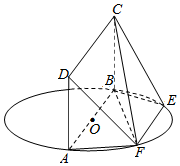 如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在平面和圆O所在的平面互相垂直.已知AB=2,EF=1.
如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在平面和圆O所在的平面互相垂直.已知AB=2,EF=1.(Ⅰ)求证:平面DAF⊥平面CBF;
(Ⅱ)设几何体F-ABCD、F-BCE的体积分别为V1、V2,求V1:V2的值.
分析 (1)由面面垂直可得AD⊥平面ABEF,从而得到AD⊥BF,由直径的性质得BF⊥AF,故得出BF⊥平面ADF,从而得出平面DAF⊥平面CBF;
(2)VF-BCE=VC-BEF,设AD=a,则可用a表示出V1,V2.从而得出体积比.
解答 证明:(1)∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,AD⊥AB,AD?平面ABCD,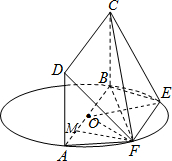
∴AD⊥平面ABEF,∵BF?平面ABE,
∴AD⊥BF,
∵AB是圆O的直径,
∴BF⊥AF,又AD?平面ADF,AF?平面ADF,AD∩AF=A,
∴BF⊥平面ADF,∵BF?平面BCF,
∴平面DAF⊥平面CBF.
(2).连结OE,OF,则OE=OF=EF=1,
∴△AOF,△OEF,△BOE是等边三角形,
过F作FM⊥AB于M,则FM=$\frac{\sqrt{3}}{2}$,FM⊥平面ABCD,
设AD=BC=a,
则V1=VF-ABCD=$\frac{1}{3}{S}_{矩形ABCD}•FM$=$\frac{1}{3}×2a×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}a}{3}$.
V2=VF-BCE=VC-BEF=$\frac{1}{3}{S}_{△BEF}•BC$=$\frac{1}{3}×\frac{1}{2}×1×\frac{\sqrt{3}}{2}×a$=$\frac{\sqrt{3}a}{12}$.
∴V1:V2=$\frac{\sqrt{3}a}{3}$:$\frac{\sqrt{3}a}{12}$=4:1.
点评 本题考查了面面垂直的性质与判定,棱锥的体积计算,属于中档题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
14.执行如图所示的程序框图,输出的n为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |