题目内容
已知a＞0且a≠1，函数f （x）=
，满足对任意实数x1≠x2，都有
＜0成立，则a的取值范围是（ ）
|
| f(x1)-f(x2) |
| x2-x1 |
| A、（0，1） | ||
| B、（1，+∞） | ||
C、（1，
| ||
D、[
|
考点：分段函数的应用
专题：计算题,函数的性质及应用
分析：由题意可知f（x）在R上为增函数，对各段考虑即有a-1＞0，即a＞1，①a＞1，②注意x=0，有（a-1）×0+3a-4≤a0，即有a≤
③，求出三个的交集即可．
| 5 |
| 3 |
解答：
解：由于f（x）=
，
又对任意实数x1≠x2，都有
＞0成立，
则f（x）在R上为增函数．
当x≤0时，函数为增，则有a-1＞0，即a＞1，①
当x＞0时，函数为增，则有a＞1，②
由在R上为增函数，则（a-1）×0+3a-4≤a0，即有a≤
③，
由①②③可得a的取值范围为：1＜a≤
．
故选C．
|
又对任意实数x1≠x2，都有
| f(x1)-f(x2) |
| x1-x2 |
则f（x）在R上为增函数．
当x≤0时，函数为增，则有a-1＞0，即a＞1，①
当x＞0时，函数为增，则有a＞1，②
由在R上为增函数，则（a-1）×0+3a-4≤a0，即有a≤
| 5 |
| 3 |
由①②③可得a的取值范围为：1＜a≤
| 5 |
| 3 |
故选C．
点评：本题考查分段函数及运用，考查函数的单调性及运用，注意各段的单调性，以及分界点的情况，属于易错题和中档题．
练习册系列答案
相关题目
平行四边形ABCD中，
•
=0，沿BD折成直二面角A-BD-C，且4AB2+2BD2=1，则三棱锥A-BCD的外接球的表面积为（ ）
| AB |
| BD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
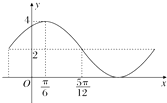已知函数y=Asin（ωx+φ）+b的一部分图象如图所示（A＞0，ω＞0，|φ|＜| π |
| 2 |
A、y=2sin（
| ||||
B、y=2sin（2x+
| ||||
C、y=4sin（2x+
| ||||
D、y=4sin（2x+
|
奇函数f（x）在（0，+∞）上的解析式为f（x）=x（1-x），则在（-∞，0）上的解析式为（ ）
| A、f（x）=x（1-x） |
| B、f（x）=x（x-1） |
| C、f（x）=x（1+x） |
| D、f（x）=-（1+x） |