Question

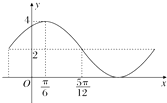已知函数y=Asin（ωx+φ）+b的一部分图象如图所示（A＞0，ω＞0，|φ|＜

π

2

），则函数表达式为（　　）

• A、y=2sin（

  1

  2

  x+

  5π

  12

  ）+2
• B、y=2sin（2x+

  π

  6

  ）+2
• C、y=4sin（2x+

  5π

  12

  ）+2
• D、y=4sin（2x+

  π

  6

  ）+2

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由y=Asin（ωx+φ）的部分图象根据正弦函数的性质先求出A，b，ω，φ的值，即可确定其解析式．

解答： 解：由题图可得

A+b=4 -A+b=0 2π ω = 5π 12 - π 6 ×4 ω• π 6 +∅= π 2

解得A=2，b=2，ω=2，φ=

π

6

，
故选：B．

点评：本题主要考查了由y=Asin（ωx+φ）的部分图象确定其解析式．考查学生基础知识的运用和图象观察能力，属于中档题．