题目内容
18.已知向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=2,|{\overrightarrow b}|=3,\overrightarrow a•({\overrightarrow b-\overrightarrow a})=1$,则$|{\overrightarrow a-\overrightarrow b}|$=( )| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{7}$ | D. | $\sqrt{23}$ |
分析 由已知的等式求出向量$\overrightarrow a,\overrightarrow b$的数量积,然后通过求$|{\overrightarrow a-\overrightarrow b}|$2再求模.
解答 解:因为向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=2,|{\overrightarrow b}|=3,\overrightarrow a•({\overrightarrow b-\overrightarrow a})=1$,所以$\overrightarrow{a}•\overrightarrow{b}=1+{\overrightarrow{a}}^{2}=5$,
则$|{\overrightarrow a-\overrightarrow b}|$=$\sqrt{{\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}}$=$\sqrt{4+9-5}=2\sqrt{2}$;
故选B
点评 本题考查了平面向量数量积公式的运用以及模的计算;属于常规题型.

练习册系列答案
相关题目
8.“a=-2”是“直线(a+2)x+3ay+1=0与直线(a-2)x+(a+2)y-3=0相互垂直”的( )条件.
| A. | 充要 | B. | 充分非必要 | ||
| C. | 必要非充分 | D. | 既非充分也非必要 |
9.一组数据X1,X2,…,Xn的平均数是3,方差是5,则数据3X1+2,3X2+2,…,3Xn+2 的平均数和方差分别是( )
| A. | 11,45 | B. | 5,45 | C. | 3,5 | D. | 5,15 |
6.下面几种推理中是演绎推理的为( )
| A. | 高二年级有21个班,1班51人,2班53人,三班52人,由此推测各班都超过50人 | |
| B. | 猜想数列$\frac{1}{1×2}$,$\frac{1}{2×3}$,$\frac{1}{3×4}$,…的通项公式为an=$\frac{1}{n(n+1)}$(n∈N+) | |
| C. | 半径为r的圆的面积S=πr2,则单位圆的面积S=π | |
| D. | 由平面三角形的性质,推测空间四面体性质 |
13.如果角α的终边经过点$({-\frac{{\sqrt{3}}}{2},\frac{1}{2}})$,那么tanα的值是( )
| A. | $-\sqrt{3}$ | B. | $-\frac{{\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
3.甲乙丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,若开始时球在甲手中,则经过三次传球后,球传回甲手中的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
10.执行如图的程序框图,则输出的n为( )
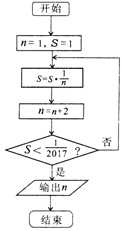

| A. | 9 | B. | 11 | C. | 13 | D. | 15 |