题目内容
3.甲乙丙三人之间相互传球,球从一个人手中随机传到另外一个人手中,若开始时球在甲手中,则经过三次传球后,球传回甲手中的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
分析 画出树状图或列表,然后根据概率公式列式进行计算即可得解.
解答 解:根据题意画出树状图如下:
∵一共有8种情况,最后球传回到甲手中的情况有2种,
∴P(球传回到甲手中)=$\frac{2}{8}$=$\frac{1}{4}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
13.若a>0,b>0,且函数f(x)=6x3-ax2-2bx+2在x=1处有极值,若t=ab,则t的最大值为( )
| A. | $\frac{81}{4}$ | B. | 6 | C. | $\frac{81}{2}$ | D. | 9 |
14.设F为抛物线y2=3x的焦点,过F且倾斜角为30°的直线l交抛物线于A(x1,y1),B(x2,y2),则|AB|=( )
| A. | 10 | B. | 6 | C. | 12 | D. | $7\sqrt{3}$ |
11.已知点P(2,1)在圆C:x2+y2+ax-2y+b=0上,点P关于直线x+y-1=0的对称点也在圆C上,则圆C的圆心坐标为( )
| A. | (0,1) | B. | (1,0) | C. | (2,1) | D. | (1,2) |
18.已知向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=2,|{\overrightarrow b}|=3,\overrightarrow a•({\overrightarrow b-\overrightarrow a})=1$,则$|{\overrightarrow a-\overrightarrow b}|$=( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{7}$ | D. | $\sqrt{23}$ |
12.“经过两条相交直线有且只有一个平面”是( )
| A. | 全称命题 | B. | 特称命题 | C. | p∨q的形式 | D. | p∧q的形式 |
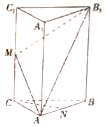 如图,在正三棱柱ABC-A1B1C1中,AB=2,M,N分别是CC1,AB的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,M,N分别是CC1,AB的中点.