题目内容
5.如图,在圆C中,弦AB的长为4,则$\overrightarrow{AB}•\overrightarrow{AC}$=( )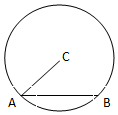
| A. | 8 | B. | -8 | C. | 4 | D. | -4 |
分析 根据平面向量数量积的定义,利用圆的垂径定理,即可求出答案.
解答 解:如图所示,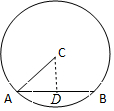
在圆C中,过点C作CD⊥AB于D,则D为AB的中点;
在Rt△ACD中,AD=$\frac{1}{2}$AB=2,
可得cosA=$\frac{AD}{AC}$=$\frac{2}{|\overrightarrow{AC}|}$,
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=|$\overrightarrow{AB}$|×|$\overrightarrow{AC}$|×cosA=4×|$\overrightarrow{AC}$|×$\frac{2}{|\overrightarrow{AC}|}$=8.
故选:A.
点评 本题考查了圆的性质、直角三角形中三角函数的定义与向量的数量积公式等知识,属于基础题.

练习册系列答案
相关题目
18.已知向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=2,|{\overrightarrow b}|=3,\overrightarrow a•({\overrightarrow b-\overrightarrow a})=1$,则$|{\overrightarrow a-\overrightarrow b}|$=( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{7}$ | D. | $\sqrt{23}$ |
13.在区间[0,2]上随机地取一个数x,则事件“-1≤log ${\;}_{\frac{1}{2}}$(x+$\frac{1}{2}$)≤1”发生的概率( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
15.函数y=Asin(ωx+ϕ)$(ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则函数表达式为( )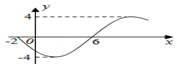

| A. | $y=-4sin(\frac{π}{8}x-\frac{π}{4})$ | B. | $y=4sin(\frac{π}{8}x-\frac{π}{4})$ | C. | $y=-4sin(\frac{π}{8}x+\frac{π}{4})$ | D. | $y=4sin(\frac{π}{8}x+\frac{π}{4})$ |
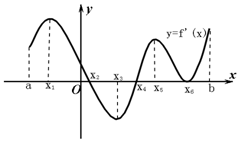 如图是导函数y=f′(x)的图象,对于函数y=f(x)的极值点的说法:?
如图是导函数y=f′(x)的图象,对于函数y=f(x)的极值点的说法:?