题目内容
设a>0,在二项式(a-
)10的展开式中,含x的项的系数与含x4的项的系数相等,则a的值为( )
| x |
| A、1 | B、2 | C、4 | D、8 |
考点:二项式定理
专题:二项式定理
分析:利用二项展开式的通项公式求出展开式的通项,令x的指数为1,4求出r的值,根据含x的项的系数与含x4的项的系数相等,代入通项求出a的值.
解答:
解:展开式的通项为Tr+1=C10ra10-r(-
)r=(-1)rC10ra10-rx
∵含x的项的系数与含x4的项的系数相等,
∴(-1)8C108a10-8=(-1)2C102a10-2,
∴a=1.
故选:A.
| x |
| r |
| 2 |
∵含x的项的系数与含x4的项的系数相等,
∴(-1)8C108a10-8=(-1)2C102a10-2,
∴a=1.
故选:A.
点评:本题考查利用二项展开式的通项公式解决二项展开式的特定项问题,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=3ex-x2ex-a在R上存在三个零点,则实数a的取值范围为( )
| A、[6e-3,2e] |
| B、(0,2e] |
| C、(-6e-3,0) |
| D、(-6e-3,2e) |
已知双曲线
-
=1的离心率为
,则n的值为( )
| x2 |
| n |
| y2 |
| 4-n |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
已知数列{an}的前n项和Sn=n2-2n,令bn=ancos
,记数列{bn}的前n项和为Tn,则T2014=( )
| nπ |
| 2 |
| A、-2011 |
| B、-2012 |
| C、-2013 |
| D、-2014 |
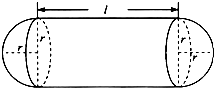 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为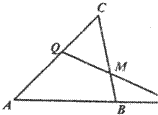 如图,在△ABC中,
如图,在△ABC中,