题目内容
若双曲线
-
=1(m>n>0)和椭圆
+
=1(m>n>0)的离心率分别为e1和e2,则e1e2的最大值为 .
| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| m2 |
| y2 |
| n2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据双曲线和椭圆离心率的定义分别求出对应的离心率,即可得到结论.
解答:
解:双曲线中a=m,b=n,c=
,双曲线的离心率e1=
=
,
椭圆中a=m,b=n,c=
,椭圆的离心率e2=
=
,
则e1e2=
•
=
=
,
∵m>n>0,
∴0<
<1,即0<(
)4<1,0<1-(
)4<1,
即0<
<1,
∴e1e2的最大值不存在,
故答案为:不存在
| m2+n2 |
| c |
| a |
| ||
| m |
椭圆中a=m,b=n,c=
| m2-n2 |
| c |
| a |
| ||
| m |
则e1e2=
| ||
| m |
| ||
| m |
|
1-(
|
∵m>n>0,
∴0<
| n |
| m |
| n |
| m |
| n |
| m |
即0<
1-(
|
∴e1e2的最大值不存在,
故答案为:不存在
点评:本题主要考查双曲线和椭圆离心率的计算,根据条件求出相应的离心率是解决本题的关键.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知数列{an}的前n项和Sn=n2-2n,令bn=ancos
,记数列{bn}的前n项和为Tn,则T2014=( )
| nπ |
| 2 |
| A、-2011 |
| B、-2012 |
| C、-2013 |
| D、-2014 |
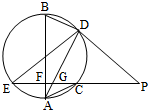 如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.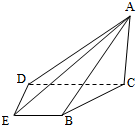 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=