题目内容
17.若实数x,y满足$\left\{\begin{array}{l}x-y+1≤0\\ x>0\\ y≤2\end{array}\right.$,则$\frac{2y}{2x+1}$的最小值是$\frac{4}{3}$.分析 由约束条件作出可行域,再由$\frac{2y}{2x+1}$=$\frac{y}{x+\frac{1}{2}}$的几何意义,即可行域内的动点与定点P($-\frac{1}{2}$,0)连线的斜率求解.
解答 解:由约束条件$\left\{\begin{array}{l}x-y+1≤0\\ x>0\\ y≤2\end{array}\right.$作出可行域,
联立$\left\{\begin{array}{l}{y=2}\\{x-y+1=0}\end{array}\right.$,解得A(1,2),
$\frac{2y}{2x+1}$=$\frac{y}{x+\frac{1}{2}}$,其几何意义为可行域内的动点与定点P($-\frac{1}{2}$,0)连线的斜率.
∵${k}_{PA}=\frac{2-0}{1+\frac{1}{2}}=\frac{4}{3}$.
∴$\frac{2y}{2x+1}$的最小值是$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
8.若从区间(0,e)(e为自然对数的底数,e=2.71828…)内随机选取两个数,则这两个数之积小于e的概率为( )
| A. | $\frac{2}{e}$ | B. | $\frac{1}{e}$ | C. | 1-$\frac{2}{e}$ | D. | 1-$\frac{1}{e}$ |
5.若函数f(x)=(ax2+bx)ex的图象如图所示,则实数a,b的值可能为( )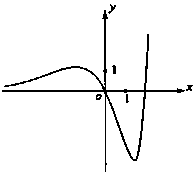

| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=2 | D. | a=-1,b=-2 |
9.一个多面体的三视图和直观图如图所示,M是AB的中点,一只蜻蜓在几何体ADF-BCE内自由飞翔,则它飞入几何体F-AMCD内的概率为( )

| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |

 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,平面ACEF⊥平面ABCD,四边形ACEF是菱形,∠CAF=60°. 已知函数f(x)=|2x-1|-2|x-1|.
已知函数f(x)=|2x-1|-2|x-1|.