题目内容
13.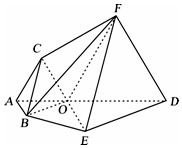 如图,ABEDEFC为多面体,平面ABED⊥平面ACED,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.
如图,ABEDEFC为多面体,平面ABED⊥平面ACED,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.(1)证明:平面OCB∥平面EFD;
(2)求直线OD与平面OEF所成角的余弦值.
分析 (1)证明:OB∥平面EFD,OC∥平面EFD,即可证明平面OCB∥平面EFD;
(2)求出D到平面OEF的距离,即可求直线OD与平面OEF所成角的余弦值.
解答  (1)证明:∵△OAB,△OAC,△ODE,△ODF都是正三角形,
(1)证明:∵△OAB,△OAC,△ODE,△ODF都是正三角形,
∴OB∥DE,OC∥DF,
∵OB?平面EFD,DE?平面EFD,OC?平面EFD,DF?平面EFD,
∴OB∥平面EFD,OC∥平面EFD,
∵OB∩OC=O,
∴平面OCB∥平面EFD;
(2)解:取OD中点G,连接EG,FG,则FG⊥AD,EG=FG=$\sqrt{3}$
∵平面ABED⊥平面ACED,平面ABED∩平面ACED=AD,
∴FG⊥平面ABED,∴FG⊥EG,
∴EF=$\sqrt{6}$,∴S△OEF=$\frac{1}{2}×\sqrt{6}×\sqrt{4-\frac{3}{2}}$=$\frac{\sqrt{15}}{2}$,
设D到平面OEF的距离为h,则$\frac{1}{3}×\frac{\sqrt{15}}{2}h=\frac{1}{3}×\frac{1}{2}×2×\sqrt{3}×\sqrt{3}$,
∴h=$\frac{2\sqrt{15}}{5}$,
∴直线OD与平面OEF所成角的正弦值=$\frac{\frac{2\sqrt{15}}{5}}{2}$=$\frac{\sqrt{15}}{5}$,
∴直线OD与平面OEF所成角的余弦值=$\sqrt{1-\frac{15}{25}}$=$\frac{\sqrt{10}}{5}$.
点评 本题考查线面平行、面面平行,考查线面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
3.从区间(0,1)中任取两个数,作为直角三角形两直角边的长,则所得的两个数列使得斜边长不大于1的概率是( )
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
4.已知a>0,曲线f(x)=2ax2-$\frac{1}{ax}$在点(1,f(1))处的切线的斜率为k,则当k取最小值时a的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
1.设a∈R,“1,a,16为等比数列”是“a=4”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
8.若从区间(0,e)(e为自然对数的底数,e=2.71828…)内随机选取两个数,则这两个数之积小于e的概率为( )
| A. | $\frac{2}{e}$ | B. | $\frac{1}{e}$ | C. | 1-$\frac{2}{e}$ | D. | 1-$\frac{1}{e}$ |
5.若函数f(x)=(ax2+bx)ex的图象如图所示,则实数a,b的值可能为( )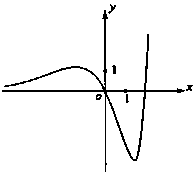

| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=2 | D. | a=-1,b=-2 |
4.若函数f(x)=a-$\frac{1}{{2}^{x}+1}$是奇函数,则实数a的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{1}{3}$ |