题目内容
19.若圆x2+y2-x+my-4=0关于直线x-y=0对称,动点P(a,b)在不等式组$\left\{\begin{array}{l}x+y-2≤0\\ x+my≥0\\ y≥0\end{array}\right.$表示的平面区域内部及边界上运动,则$z=\frac{b-2}{a-1}$的取值范围是(-∞,-2]∪[2,+∞).分析 由已知列式求得m值,代入约束条件,作出可行域,结合$z=\frac{b-2}{a-1}$的几何意义,即区域OAB内点P(a,b)与点Q(1,2)连线的斜率求解.
解答 解:∵圆x2+y2-x+my-4=0关于直线x-y=0对称,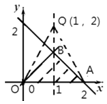
∴圆心$(\frac{1}{2},-\frac{m}{2})$在直在线x-y=0上,则$\frac{1}{2}=-\frac{m}{2}⇒m=-1$,
约束条件$\left\{\begin{array}{l}x+y-2≤0\\ x-y≥0\\ y≥0\end{array}\right.$表示的平面区域如图:
$z=\frac{b-2}{a-1}$表示区域OAB内点P(a,b)与点Q(1,2)连线的斜率.
∵${K_{OQ}}=\frac{2-0}{1-0}=2$,${K_{AQ}}=\frac{0-2}{2-1}=-2$,
∴$z=\frac{b-2}{a-1}$的取值范围是(-∞,-2]∪[2,+∞).
故答案为:(-∞,-2]∪[2,+∞).
点评 本题考查简单的线性规划,考查数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
相关题目
4.已知a>0,曲线f(x)=2ax2-$\frac{1}{ax}$在点(1,f(1))处的切线的斜率为k,则当k取最小值时a的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
11.若集合A={-2,-1,0,1,2},集合B={x|lg(x+1)>0},则A∩B等于( )
| A. | {-1,0,1,2} | B. | {-1,-2} | C. | {1,2} | D. | {0,1,2} |
8.若从区间(0,e)(e为自然对数的底数,e=2.71828…)内随机选取两个数,则这两个数之积小于e的概率为( )
| A. | $\frac{2}{e}$ | B. | $\frac{1}{e}$ | C. | 1-$\frac{2}{e}$ | D. | 1-$\frac{1}{e}$ |
9.一个多面体的三视图和直观图如图所示,M是AB的中点,一只蜻蜓在几何体ADF-BCE内自由飞翔,则它飞入几何体F-AMCD内的概率为( )

| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
 在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点D为BC的中点;
在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点D为BC的中点;