题目内容
3.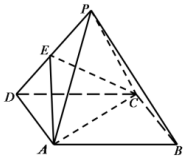 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且平面PAC⊥平面ABCD,E为PD的中点,PA=PC,AB=2BC=2,∠ABC=60°.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且平面PAC⊥平面ABCD,E为PD的中点,PA=PC,AB=2BC=2,∠ABC=60°.(Ⅰ)求证:PB∥平面ACE;
(Ⅱ)求证:平面PBC⊥平面PAC.
分析 (Ⅰ)连接BD,交AC于点O,连接OE,证明OE∥PB,即可证明PB∥平面ACE;
(Ⅱ)证明BC⊥平面PAC,即可证明:平面PBC⊥平面PAC.
解答 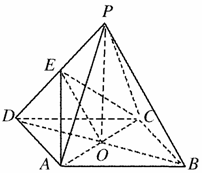 证明:(Ⅰ)连接BD,交AC于点O,连接OE,
证明:(Ⅰ)连接BD,交AC于点O,连接OE,
∵底面ABCD是平行四边形,∴O为BD中点,
又E为PD中点,∴OE∥PB,
又OE?平面ACE,PB?平面ACE,
∴PB∥平面ACE.
(Ⅱ)∵PA=PC,O为AC中点,∴PO⊥AC,
又平面PAC⊥平面ABCD,
平面PAC∩平面ABCD=AC,PO?平面PAC,
∴PO⊥平面ABCD,
又BC?平面ABCD,
∴PO⊥BC.
在△ABC中,AB=2BC=2,∠ABC=60°,
∴$AC=\sqrt{A{B^2}+B{C^2}-2AB•BC•cos∠ABC}$=$\sqrt{{2^2}+{1^2}-2×2×1×\frac{1}{2}}=\sqrt{3}$,
∴AC2=AB2+BC2,∴BC⊥AC.
又PO?平面PAC,AC?平面PAC,PO∩AC=O,∴BC⊥平面PAC,
又BC?平面PBC,∴平面PBC⊥平面PAC.
点评 本题考查线面平行的判定,线面垂直的判定,熟练掌握线线、线面、面面垂直之间的相互转化是关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
11.若集合A={-2,-1,0,1,2},集合B={x|lg(x+1)>0},则A∩B等于( )
| A. | {-1,0,1,2} | B. | {-1,-2} | C. | {1,2} | D. | {0,1,2} |
8.若从区间(0,e)(e为自然对数的底数,e=2.71828…)内随机选取两个数,则这两个数之积小于e的概率为( )
| A. | $\frac{2}{e}$ | B. | $\frac{1}{e}$ | C. | 1-$\frac{2}{e}$ | D. | 1-$\frac{1}{e}$ |
 在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点D为BC的中点;
在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,点D为BC的中点;