题目内容
下列函数中,既是奇函数,又是减函数的是( )
A、y=x
| ||
| B、y=2|x| | ||
C、y=
| ||
| D、y=2-x-2x |
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:根据函数奇偶性和单调性的性质即可得到结论
解答:
解:A.y=x
是奇函数,也是单调递减函数,满足条件,
B.y=2|x|是偶函数,在定义域上不是单调函数,不满足条件,
C.y=
是奇函数,在定义域上不是单调函数,不满足条件,
D.f(x)=2-x-2x,则f(-x)=2x-2-x=-f(x),为奇函数,在定义域上为增函数,不满足条件.
故选:A
| 1 |
| 3 |
B.y=2|x|是偶函数,在定义域上不是单调函数,不满足条件,
C.y=
| 1 |
| x |
D.f(x)=2-x-2x,则f(-x)=2x-2-x=-f(x),为奇函数,在定义域上为增函数,不满足条件.
故选:A
点评:本题主要考查函数奇偶性和单调性的判断,要求熟练掌握常见函数的奇偶性和单调性的性质.

练习册系列答案
相关题目
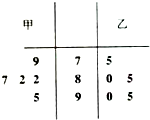 甲、乙两位同学参加数学竞赛培训,在培训期间,他们参加的5次预赛成绩数据茎叶图如图,下列对提供的数据分析正确的是( )
甲、乙两位同学参加数学竞赛培训,在培训期间,他们参加的5次预赛成绩数据茎叶图如图,下列对提供的数据分析正确的是( )A、
| ||||
B、
| ||||
| C、S甲2>S乙2 | ||||
| D、S甲2<S乙2 |
在空间直角坐标系中,点P在x轴正半轴上,它到Q(0,
,3)的距离为2
,则点P的坐标为( )
| 2 |
| 3 |
| A、(2,0,0) |
| B、(-1,0,0) |
| C、(0,0,1) |
| D、(1,0,0) |
“x<2”是“x2<4”的( )
| A、必要不充分条件 |
| B、充要条件 |
| C、充分不必要条件 |
| D、既不充分又非必要条件 |
阅读如图所示的程序框图,则输出的S的值为( )


A、-
| ||||
| B、0 | ||||
C、
| ||||
D、
|
设x>0,y>0,则(x+y)(
+
)的最小值为( )
| 1 |
| x |
| 4 |
| y |
| A、7 | B、8 | C、9 | D、10 |
已知函数f(x)=xlnx,则其在点(e,f(e))处的切线方程是( )
| A、y=2x-e | B、y=e |
| C、y=x-e | D、y=x+e |
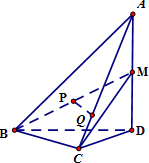 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.