题目内容
对于任意给定的实数m,直线3x-y+m=0与双曲线
-
=1(a>0,b>0)最多有一个交点,则双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
| C、3 | ||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题意可知,直线3x-y+m=0与双曲线的其中一条渐近线重合或平行,根据斜率之间的关系,即可求出a,c之间的关系,即可求出双曲线的离心率.
解答:
解:由题意可知,直线3x-y+m=0与双曲线的其中一条渐近线重合或平行,
那么这条渐近线方程的斜率为3,即
=3,
则b=3a,
则c=
=
=
a,
则双曲线的离心率e=
=
,
故选:D
那么这条渐近线方程的斜率为3,即
| b |
| a |
则b=3a,
则c=
| a2+b2 |
| a2+9a2 |
| 10 |
则双曲线的离心率e=
| c |
| a |
| 10 |
故选:D
点评:本题主要考查双曲线离心率的计算,根据双曲线渐近线的性质建立条件关系得到a,c的关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为了解800名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为( )
| A、50 | B、40 | C、25 | D、20 |
下列函数中,既是奇函数,又是减函数的是( )
A、y=x
| ||
| B、y=2|x| | ||
C、y=
| ||
| D、y=2-x-2x |
关于复数z=1+
(i是虚数单位),下列表述正确的是( )
| 1 |
| (1+i)2 |
| A、z是纯虚数 |
| B、z是实数 |
| C、z的虚部是1 |
| D、在复平面内z对应的点在第四象限 |
已知(1-2x)2014=a0+a1x+a2x2+…+a2014x2014,则a0+a1+a2+…+a2014=( )
| A、22014 |
| B、32013 |
| C、1 |
| D、-1 |
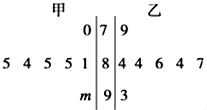 如图是某青年歌手大奖赛是七位评委为甲、乙两名选手打分的茎叶图(其中m是数字0~9中的一个),去掉一个最高分和一个最低分之后,甲、乙两名选手的方差分别是a1和a2,则( )
如图是某青年歌手大奖赛是七位评委为甲、乙两名选手打分的茎叶图(其中m是数字0~9中的一个),去掉一个最高分和一个最低分之后,甲、乙两名选手的方差分别是a1和a2,则( )| A、a1>a2 |
| B、a1<a2 |
| C、a1=a2 |
| D、a1,a2的大小与m的值有关 |
圆内接四边形ABCD中,∠A,∠B,∠C的度数的比是3:4:6,则∠D=( )
| A、60° | B、80° |
| C、120° | D、100° |
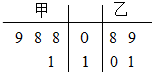 甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.
甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.