题目内容
在空间直角坐标系中,点P在x轴正半轴上,它到Q(0,
,3)的距离为2
,则点P的坐标为( )
| 2 |
| 3 |
| A、(2,0,0) |
| B、(-1,0,0) |
| C、(0,0,1) |
| D、(1,0,0) |
考点:空间中的点的坐标
专题:空间位置关系与距离
分析:根据点P在x轴上,设出点P的坐标,再根据P到Q的距离,列出方程,解方程即可求得P的坐标.
解答:
解:设P(x,0,0),x>0,
由x2+(0-
)2+32=(2
)2,
可得x=1
故P(1,0,0)
故选:D.
由x2+(0-
| 2 |
| 3 |
可得x=1
故P(1,0,0)
故选:D.
点评:考查空间两点间的距离公式,空间两点的距离公式和平面中的两点距离公式相比较记忆,利于知识的系统化,属基础题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
为了解800名学生的学习情况,采用系统抽样的方法,从中抽取容量为40的样本,则分段的间隔为( )
| A、50 | B、40 | C、25 | D、20 |
要得到函数y=f′(x)的图象,需将函数f(x)=sinx-cosx(x∈R)的图象( )
A、向左平移
| ||
B、向右平移
| ||
| C、向左平移π个单位 | ||
| D、向右平移π个单位 |
已知集合A={0,1,2},B={x|1<x<4},则A∩B=( )
| A、{0} | B、{1} |
| C、{2} | D、{1,2} |
下列函数中,既是奇函数,又是减函数的是( )
A、y=x
| ||
| B、y=2|x| | ||
C、y=
| ||
| D、y=2-x-2x |
圆内接四边形ABCD中,∠A,∠B,∠C的度数的比是3:4:6,则∠D=( )
| A、60° | B、80° |
| C、120° | D、100° |
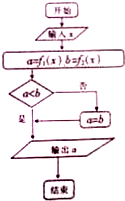 已知函数f1(x)=x,f2(x)=
已知函数f1(x)=x,f2(x)=