题目内容
已知函数f（x）=xlnx，则其在点（e，f（e））处的切线方程是（ ）
| A、y=2x-e | B、y=e |
| C、y=x-e | D、y=x+e |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：先求导函数，然后将x=e代入导函数，从而求出在点x=e处的斜率，再结合曲线上一点求出切线方程．
解答：
解：∵y=xlnx，
∴y′=lnx+1，
∴x=e时，y′=lne+1=2，
又当x=e时y=e，即切点为（e，e），
∴切线方程为y-e=2（x-e）即y=2x-e．
故选：A．
∴y′=lnx+1，
∴x=e时，y′=lne+1=2，
又当x=e时y=e，即切点为（e，e），
∴切线方程为y-e=2（x-e）即y=2x-e．
故选：A．
点评：本题考查导数的几何意义，考查学生的计算能力，正确求导是关键．学生在解决此类问题一定要分清“在某点处的切线”，还是“过某点的切线”；同时解决“过某点的切线”问题，一般是设出切点坐标解决．属于基础题．
练习册系列答案
53随堂测系列答案
相关题目
要得到函数y=f′（x）的图象，需将函数f（x）=sinx-cosx（x∈R）的图象（ ）
A、向左平移
| ||
B、向右平移
| ||
| C、向左平移π个单位 | ||
| D、向右平移π个单位 |
下列函数中，既是奇函数，又是减函数的是（ ）
A、y=x
| ||
| B、y=2|x| | ||
C、y=
| ||
| D、y=2-x-2x |
已知（1-2x）2014=a0+a1x+a2x2+…+a2014x2014，则a0+a1+a2+…+a2014=（ ）
| A、22014 |
| B、32013 |
| C、1 |
| D、-1 |
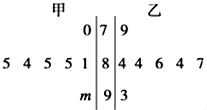如图是某青年歌手大奖赛是七位评委为甲、乙两名选手打分的茎叶图（其中m是数字0～9中的一个），去掉一个最高分和一个最低分之后，甲、乙两名选手的方差分别是a1和a2，则（ ）| A、a1＞a2 |
| B、a1＜a2 |
| C、a1=a2 |
| D、a1，a2的大小与m的值有关 |
函数y=2sin2x的图象的一条对称轴方程是（ ）
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
圆内接四边形ABCD中，∠A，∠B，∠C的度数的比是3：4：6，则∠D=（ ）
| A、60° | B、80° |
| C、120° | D、100° |