题目内容
已知数列{an}共有2k项(整数k≥2),数列{an}的前n项的和为Sn,满足a1=2,an+1=(a-1)Sn+2(n=1,2,…,2k-1),其中常数a>1,求证{an}为等比数列.
考点:等比关系的确定
专题:等差数列与等比数列
分析:由an+1=(a-1)Sn+2(n=1,2,…,2k-1),当n≥2时,an=(a-1)Sn-1+2,两式相减可得:an+1=a•an.即可证明.
解答:
证明:∵an+1=(a-1)Sn+2(n=1,2,…,2k-1),
∴当n≥2时,an=(a-1)Sn-1+2,
两式相减可得:an+1-an=(a-1)an,化为an+1=a•an.
又a2=2(a-1)+2=2a=2a1.
∵a1=2,a>1.
∴{an}为等比数列.
∴当n≥2时,an=(a-1)Sn-1+2,
两式相减可得:an+1-an=(a-1)an,化为an+1=a•an.
又a2=2(a-1)+2=2a=2a1.
∵a1=2,a>1.
∴{an}为等比数列.
点评:本题考查了递推式的意义、等比数列的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=lnx-
的零点所在的区间为( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
已知抛物线的方程为y2=2x,则其焦点坐标为( )
A、(0,
| ||
B、(
| ||
C、(±
| ||
D、(0,-
|
函数y=
(a>1)的图象的大致形状是( )
| |x| |
| xax |
A、 |
B、 |
C、 |
D、 |
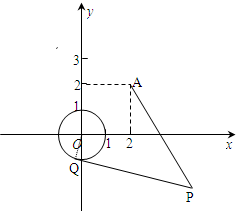 如图,已知⊙O:x2+y2=1和定点A(2,2),由⊙O外一点P(a,b)向⊙O引切线PQ,Q为切点,且满足|PQ|=|PA|.
如图,已知⊙O:x2+y2=1和定点A(2,2),由⊙O外一点P(a,b)向⊙O引切线PQ,Q为切点,且满足|PQ|=|PA|.