题目内容
若函数f(x)是定义域D内的某个区间I上的增函数,且F(x)=
在I上是减函数,则称y=f(x)是I上的“非完美增函数”,已知f(x)=lnx,g(x)=2x+
+alnx(a∈R)
(1)判断f(x)在(0,1]上是否是“非完美增函数”;
(2)若g(x)是[1,+∞)上的“非完美增函数”,求实数a的取值范围.
| f(x) |
| x |
| 2 |
| x |
(1)判断f(x)在(0,1]上是否是“非完美增函数”;
(2)若g(x)是[1,+∞)上的“非完美增函数”,求实数a的取值范围.
考点:利用导数研究函数的单调性,奇偶性与单调性的综合
专题:导数的综合应用
分析:(1)依据“非完美增函数”的定义判断即可;
(2)由题意可得g(x)在[1,+∞)上为增函数,G(x)=
=2+
+
在[1,+∞)上是减函数,利用导数研究函数的单调性,即可求得结论.
(2)由题意可得g(x)在[1,+∞)上为增函数,G(x)=
| g(x) |
| x |
| 2 |
| x2 |
| alnx |
| x |
解答:
解:(1)由于f(x)=lnx,在(0,1]上是增函数,且F(x)=
=
,
∵F′(x)=
,∴当x∈(0,1]时,F′(x)>0,F(x)为增函数,
∴f(x)在(0,1]上不是“非完美增函数”;
(2)∵g(x)=2x+
+alnx,
∴g′(x)=2-
+
=
,
∵g(x)是[1,+∞)上的“非完美增函数”,
∴g′(x)≥0在[1,+∞)上恒成立,
∴g′(1)≥0,∴a≥0,
又G(x)=
=2+
+
在[1,+∞)上是减函数,
∴G′(x)≤0在[1,+∞)恒成立,即-
+
≤0在[1,+∞)恒成立,
即ax-axlnx-4≤0在[1,+∞)恒成立,
令p(x)=ax-axlnx-4,则p′(x)=-alnx≤0恒成立(∵a≥0,x≥1),
∴p(x)=ax-axlnx-4在[1,+∞)上单调递减,
∴p(x)max=p(1)=a-4≤0,解得:a≤4;
综上所述0≤a≤4.
| f(x) |
| x |
| lnx |
| x |
∵F′(x)=
| 1-lnx |
| x2 |
∴f(x)在(0,1]上不是“非完美增函数”;
(2)∵g(x)=2x+
| 2 |
| x |
∴g′(x)=2-
| 2 |
| x2 |
| a |
| x |
| 2x2+ax-2 |
| x2 |
∵g(x)是[1,+∞)上的“非完美增函数”,
∴g′(x)≥0在[1,+∞)上恒成立,
∴g′(1)≥0,∴a≥0,
又G(x)=
| g(x) |
| x |
| 2 |
| x2 |
| alnx |
| x |
∴G′(x)≤0在[1,+∞)恒成立,即-
| 4 |
| x3 |
| a(1-lnx) |
| x2 |
即ax-axlnx-4≤0在[1,+∞)恒成立,
令p(x)=ax-axlnx-4,则p′(x)=-alnx≤0恒成立(∵a≥0,x≥1),
∴p(x)=ax-axlnx-4在[1,+∞)上单调递减,
∴p(x)max=p(1)=a-4≤0,解得:a≤4;
综上所述0≤a≤4.
点评:本题以新定义的形式考查函数的单调性,考查运用所学知识分析解决新问题的能力.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
如图,E为正方体的棱AA1的中点,F为棱AB上的一点,且∠C1EF=90°,则AF:FB=( )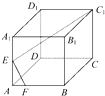

| A、1:1 | B、1:2 |
| C、1:3 | D、1:4 |
若a,b∈R,则下列命题正确的是( )
| A、若a>b,则a2>b2 | ||||
B、若a>b,则
| ||||
| C、若a>|b|,则a2>b2 | ||||
| D、若ac>bc,则a>b |
下列四个方程中表示y是x的函数的是( )
①x-2y=6②x2+y=1③x+y2=1④x=
.
①x-2y=6②x2+y=1③x+y2=1④x=
| y |
| A、①② | B、①④ | C、③④ | D、①②④ |
函数y=
x4-x3的极值点的个数为( )
| 3 |
| 4 |
| A、0个 | B、1个 | C、2个 | D、3个 |
执行下面的程序框图,若输出的结果是2,则①处应填入的是( )

| A、x=2 | B、x=1 |
| C、b=2 | D、a=5 |