题目内容
已知f(x)=3x2-4x+5,g(x)=f(x-2),则g(3)= .
考点:函数的值
专题:函数的性质及应用
分析:由g(x)=f(x-2)得g(3)=f(1),代入f(x)的解析式求出值.
解答:
解:∵g(x)=f(x-2),
∴g(3)=f(3-2)=f(1)=3-4+5=4
故答案为:4;
∴g(3)=f(3-2)=f(1)=3-4+5=4
故答案为:4;
点评:本题考查由解析式求函数值,属于一道基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
函数y=
的单调递增区间为( )
| x2-3x+2 |
A、[
| ||
B、(-∞,
| ||
| C、[2,+∞) | ||
| D、(-∞,1] |
函数f(x)=
,若0<f (x0)<1,则x0的取值范围是( )
|
| A、[1,+∞) |
| B、(1,+∞) |
| C、(-∞,1] |
| D、(0,+∞) |
已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是棱AB,BC上的点,且AE=BF,若A1E与C1F所成的角最小,则有( )
A、AE=BF=
| ||
B、AE=BF=
| ||
C、AE=BF=
| ||
D、AE=BF=
|
如图,E为正方体的棱AA1的中点,F为棱AB上的一点,且∠C1EF=90°,则AF:FB=( )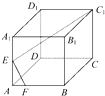

| A、1:1 | B、1:2 |
| C、1:3 | D、1:4 |
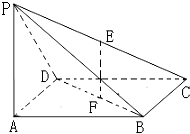 如图在四棱锥P-ABCD中,底面abcd是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图在四棱锥P-ABCD中,底面abcd是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=