题目内容
已知f(x)=(1+2x)(1+x)5,则导函数的展开式中x2的系数是 .
考点:二项式定理的应用,导数的运算
专题:导数的概念及应用,二项式定理
分析:根据导数的定义先求导,再根据二项式展开定理求出x2的系数
解答:
解:∵f(x)=(1+2x)(1+x)5,
∴f′(x)=2(1+x)5+5(1+2x)(1+x)4,
∵二项式(1+x)n的展开式通项是Tr+1=
•xr,
∴2(1+x)5的展开式中x2的系数是2
=20,
5(1+2x)(1+x)4展开式中x2的系数是5(
+2
)=70,
故导函数的展开式中x2的系数是20+70=90,
故答案为:90
∴f′(x)=2(1+x)5+5(1+2x)(1+x)4,
∵二项式(1+x)n的展开式通项是Tr+1=
| C | r n |
∴2(1+x)5的展开式中x2的系数是2
| C | 2 5 |
5(1+2x)(1+x)4展开式中x2的系数是5(
| C | 2 4 |
| C | 1 4 |
故导函数的展开式中x2的系数是20+70=90,
故答案为:90
点评:本题考查了导数的运算法则和二项式定理,属于基础题

练习册系列答案
相关题目
将3张不同的奥运门票分给10名同学中的3人,每人1张,则不同的分法有( )
| A、2610种 | B、720种 |
| C、240种 | D、60种 |
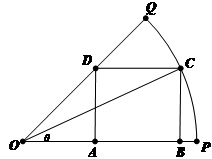 如图,在半径为40cm、圆心角为60°的扇形铝皮OPQ上截取一块矩形材料ABCD,其中点A,B在OP上,点C在
如图,在半径为40cm、圆心角为60°的扇形铝皮OPQ上截取一块矩形材料ABCD,其中点A,B在OP上,点C在