题目内容
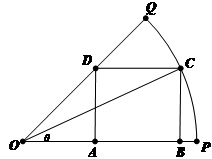 如图,在半径为40cm、圆心角为60°的扇形铝皮OPQ上截取一块矩形材料ABCD,其中点A,B在OP上,点C在
如图,在半径为40cm、圆心角为60°的扇形铝皮OPQ上截取一块矩形材料ABCD,其中点A,B在OP上,点C在 |
| PQ |
(1)设∠COP=θ,将边AB,BC表示成θ的关系式;
(2)怎样截取才能使截得的矩形ABCD的面积最大?并求出最大面积.
考点:弧度制的应用
专题:应用题,三角函数的图像与性质
分析:(1)先把矩形的各个边长用角θ表示出来,进而表示出矩形的面积即可将边AB,BC表示成θ的关系式;
(2)再利用角θ的范围,结合正弦函数的性质可求求矩形面积的最大值即可.
(2)再利用角θ的范围,结合正弦函数的性质可求求矩形面积的最大值即可.
解答:
解:在RT△OBC中,OB=OC•cosθ=40cosθ,BC=OC•sinθ=40sinθ
在RT△OAD中,
=tan60°=
(2分)
∴OA=
DA=
BC=40
sinθ,
∴AB=OB-OA=40cosθ-40
sinθ,(4分)
矩形ABCD的面积S=AB•BC=(40cosθ-40
sinθ)40sinθ=1600sinθcosθ-1600
sin2θ=800sin2θ-1600
(1-cos2θ)=800sin2θ+1600
cos2θ-1600
=1600
(
sin2θ+
cos2θ)-1600
=1600
sin(2θ+
)-1600
(8分)
(2)由0<θ<
,得
<2θ+
<
,(10分)
所以当2θ+
=
,即θ=
时,(12分)
S最大=
-
=
,
所以,当θ=
时,矩形ABCD的面积最大,最大面积为
.(14分)
在RT△OAD中,
| DA |
| OA |
| 3 |
∴OA=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
∴AB=OB-OA=40cosθ-40
| ||
| 3 |
矩形ABCD的面积S=AB•BC=(40cosθ-40
| ||
| 3 |
| ||
| 3 |
| ||
| 6 |
| ||
| 6 |
| ||
| 6 |
| 1 | ||
|
| ||
| 2 |
| 1 |
| 2 |
| ||
| 6 |
| 1 | ||
|
| π |
| 6 |
| ||
| 6 |
(2)由0<θ<
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
所以当2θ+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
S最大=
| 1 | ||
|
| ||
| 6 |
| ||
| 6 |
所以,当θ=
| π |
| 6 |
| ||
| 6 |
点评:本题考查在实际问题中建立三角函数模型,求解问题的关键是根据图形建立起三角模型,将三角模型用所学的恒等式变换公式进行化简,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知
=(1,-
,
),
=(-3,λ,-
)满足
∥
,则λ等于( )
| a |
| 3 |
| 2 |
| 5 |
| 2 |
| b |
| 15 |
| 2 |
| a |
| b |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知函数f(x)中,f(1)=0,且对任意正整数x满足f(x+1)=f(x)+2x,则f(2012)=( )
| A、2010×2011 |
| B、20112 |
| C、2011×2012 |
| D、20122 |
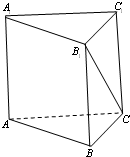 如图,正三棱柱的底面边长为1,体积为
如图,正三棱柱的底面边长为1,体积为