题目内容
命题p:?x∈R,cos2x+sinx≥2m2-m-7;命题q:mx2+2x-1>o的解集非空.若“p且q”是假命题,┐p也是假命题,则实数m的取值范围: .
考点:复合命题的真假
专题:函数的性质及应用,简易逻辑
分析:本题考查复合命题的真假判定,由┐p是假命题得p是真命题,而“p且q”是假命题,则q为假命题,然后分别求解p为真命题:cos2x+sinx=1-sin2x+sinx最小值是-1,2m2-m-7≤-1,解得-32≤m≤2;
由q为假命题得mx2+2x-1>0的解集为空集,解得,-32≤m≤-1,求交集.
由q为假命题得mx2+2x-1>0的解集为空集,解得,-32≤m≤-1,求交集.
解答:
解:┐p是假命题,则p是真命题,而“p且q”是假命题,则q为假命题,
令f(x)=cos2x+sinx=1-sin2x+sinx,
∵x∈R,sinx∈[-1,1],当x=-1时取得最小值-1,
则2m2-m-7≤-1,解得-
≤m≤2,
由q为假命题得mx2+2x-1>0的解集为空集,则
,即m≤-1
综上,-
≤m≤-1.
故答案为:-
≤m≤-1
令f(x)=cos2x+sinx=1-sin2x+sinx,
∵x∈R,sinx∈[-1,1],当x=-1时取得最小值-1,
则2m2-m-7≤-1,解得-
| 3 |
| 2 |
由q为假命题得mx2+2x-1>0的解集为空集,则
|
综上,-
| 3 |
| 2 |
故答案为:-
| 3 |
| 2 |
点评:掌握复合命题真假判断的关键;p或q:一真为真;p且q:一假为假;p与非P:真假相反.

练习册系列答案
相关题目
执行如图的程序框图,输出的结果为( )
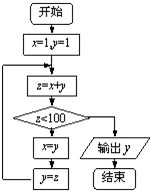

| A、55 | B、89 |
| C、144 | D、233 |
已知全集U=R,M={x|x>1},N={x|x≤-1,或x≥5},则M∩(∁UN)=( )
| A、{x|1<x≤5} |
| B、{x|1<x<5} |
| C、{x|-1<x<5} |
| D、∅ |
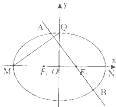 已知椭圆C:
已知椭圆C: